Método Gráfico para Programación Lineal#
El Método Gráfico es una técnica intuitiva para resolver problemas de programación lineal con dos variables. Permite visualizar las restricciones y la región factible, facilitando la identificación de la solución óptima.
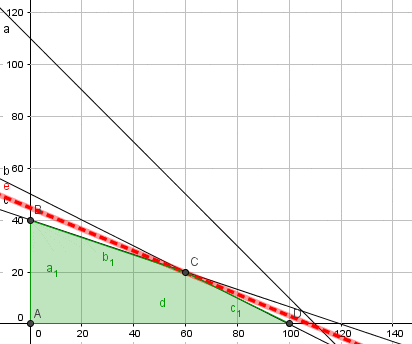
Algoritmo del Método Gráfico#
El proceso para aplicar el método gráfico incluye:
Representación de Restricciones: Dibujar las restricciones del problema en un plano bidimensional.
Región Factible: Identificar la región factible donde se cumplen todas las restricciones.
Puntos extremos: Encontrar los puntos extremos del área.
Reemplazar en la función objetivo: Reemplazar en la función objetivo y encontrar la solución.
Tipos de soluciones:#
Solución Óptima Única: Este es el caso más común y deseado. Ocurre cuando el algoritmo encuentra un único punto que maximiza o minimiza la función objetivo dentro de la región factible. Este resultado se da cuando existe un vértice de la región factible que proporciona el valor más alto o más bajo de la función objetivo, y no hay otros puntos con el mismo valor.
Soluciones Múltiples (o Degeneradas): En este escenario, hay más de un punto óptimo. Esto significa que existen múltiples vértices en la región factible que proporcionan el mismo valor óptimo para la función objetivo. A menudo, esto ocurre en problemas donde la función objetivo es paralela a una de las restricciones del problema.
Problema No Acotado: Sucede cuando la región factible es abierta en la dirección en la que se está optimizando la función objetivo. En otras palabras, no hay un límite en el valor de la función objetivo; puede ir al infinito. Esto generalmente ocurre cuando las restricciones no confinan completamente la región factible en la dirección de optimización.
Solución Inexistente: Se da cuando no hay una región factible, es decir, el conjunto de restricciones es tal que no hay ningún punto que satisfaga todas las restricciones al mismo tiempo. Esto puede suceder si las restricciones se contradicen entre sí.
Ciclo Infinito (menos común): Aunque raro y generalmente evitado mediante técnicas como la regla de Bland, teóricamente es posible que el método simplex entre en un ciclo infinito, rotando entre un conjunto de soluciones sin llegar nunca a una conclusión. Esto puede ocurrir en ciertas situaciones particulares donde el algoritmo no logra avanzar hacia una solución óptima debido a la naturaleza de las restricciones y la función objetivo.
Pasos del Método Gráfico#
Definir Restricciones: El primer paso es definir las restricciones del problema. Estas restricciones son representadas por ecuaciones o inecuaciones lineales.
Representación Gráfica: Cada restricción se representa gráficamente en un plano bidimensional. Esto se realiza trazando las líneas correspondientes a cada ecuación.
Región Factible: La intersección de todas las restricciones forma la región factible. Es el conjunto de todos los puntos que satisfacen todas las restricciones.
Puntos clave: Se extraen los vertices en los que se ubica la región factible.
Solución Óptima: El punto donde la función objetivo es óptima (ya sea máxima o mínima) y que sigue siendo parte de la región factible es la solución al problema de programación lineal.
Ejemplo:#
La función objetivo que se busca maximizar podría ser, por ejemplo, $\( z=3x+2y \)$
Sujeto a las siguientes restricciones
La primera restricción es: \(x+2y≤20\).
La segunda restricción es: \(3x+4y≥12\).
import sympy as sp
import matplotlib.pyplot as plt
import numpy as np
x, y = sp.symbols('x y')
restriccion1 = x + 2*y - 20
restriccion2 = 3*x + 4*y - 12
# Configurar el rango para las variables
x_vals = np.linspace(0, 30, 100)
# Convertir restricciones a funciones para y
y_restriccion1 = sp.solve(restriccion1, y)[0]
y_restriccion2 = sp.solve(restriccion2, y)[0]
# Convertir a funciones numéricas
func_restriccion1 = sp.lambdify(x, y_restriccion1, modules=['numpy'])
func_restriccion2 = sp.lambdify(x, y_restriccion2, modules=['numpy'])
# Graficar las restricciones
plt.plot(x_vals, func_restriccion1(x_vals), label=sp.latex(restriccion1))
plt.plot(x_vals, func_restriccion2(x_vals), label=sp.latex(restriccion2))
plt.xlim(0, 30)
plt.ylim(0, 30)
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.axhline(0, color='black', lw=2)
plt.axvline(0, color='black', lw=2)
plt.fill_between(x_vals, func_restriccion1(x_vals), func_restriccion2(x_vals), where=(x_vals <= 30), color='gray', alpha=0.3,label="Región Factible")
plt.legend()
plt.show()
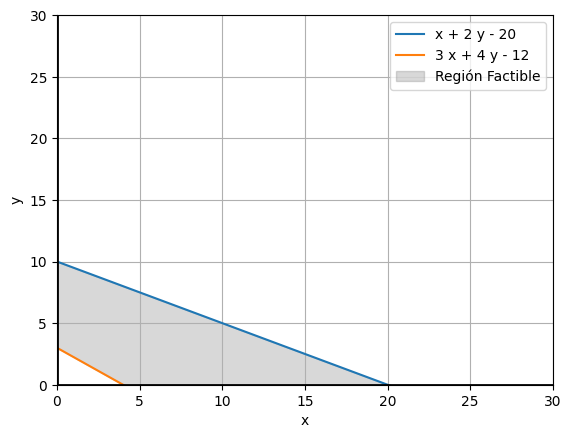
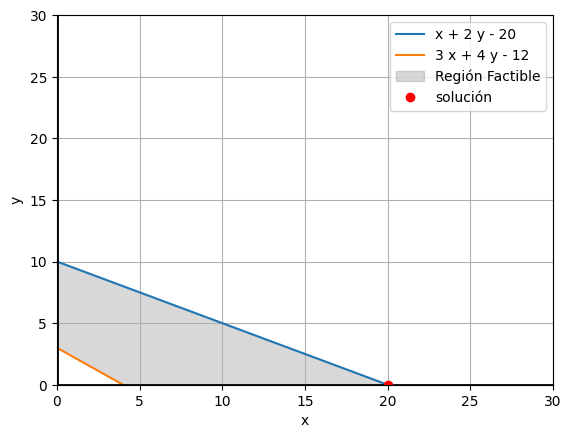
El área sombreada representa la región factible. La solución óptima se encuentra en uno de los vértices de esta región. En un caso real, también graficarías la función objetivo y la moverías paralelamente hasta encontrar el punto óptimo en la región factible.
Este proceso muestra cómo se puede implementar y visualizar el método gráfico en programación lineal, facilitando la comprensión y análisis del problema.
# Configurar el rango para las variables
x_vals = np.linspace(0, 30, 100)
# Convertir restricciones a funciones para y
y_restriccion1 = sp.solve(restriccion1, y)[0]
y_restriccion2 = sp.solve(restriccion2, y)[0]
# Convertir a funciones numéricas
func_restriccion1 = sp.lambdify(x, y_restriccion1, modules=['numpy'])
func_restriccion2 = sp.lambdify(x, y_restriccion2, modules=['numpy'])
# Graficar las restricciones
plt.plot(x_vals, func_restriccion1(x_vals), label=sp.latex(restriccion1))
plt.plot(x_vals, func_restriccion2(x_vals), label=sp.latex(restriccion2))
plt.xlim(0, 30)
plt.ylim(0, 30)
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.axhline(0, color='black', lw=2)
plt.axvline(0, color='black', lw=2)
plt.fill_between(x_vals, func_restriccion1(x_vals), func_restriccion2(x_vals), where=(x_vals <= 30), color='gray', alpha=0.3,label="Región Factible")
vertices = [
(0,3),
(4,0),
(0,10),
(20,0)
]
optimo = max(vertices, key=lambda punto: 3*punto[0] + 2*punto[1])
plt.plot(optimo[0], optimo[1], 'ro', label="solución")
plt.legend()
plt.show()
Ejercicio#
Resuelva el siguiente problema usando el metodo gráfico
sujeto a:
Tarea#
Implementar el código para generalizar el método gráfico, para N restricciones y para que el usuario pueda ingresar los vértices.
## Tu código va acá
## Hasta acá
Formulación de problemas de programación lineal: Ejercicio 1#
Un artesano produce cestas y sombreros de mimbre. Por cada cesta gana $2000 y por cada sombrero $3000. Para hacer una cesta o un sombrero utiliza \(1m^2\) de mimbre y en total se dispone de \(80m^2\) de mimbre. 1 cesta requiere una hora hombre y 1 sombrero 2 horas hombre. Se disponen de 100 horas. Por razones de almacenamiento, se pueden fabricar como máximo 70 cestas. Plantear el PPL y resolverlo mendiante método simplex.
Formulación de problemas de programación lineal: Ejercicio 2#
La empresa X ha sacado del mercado un producto que ya no era rentable, lo cual genera que haya una capacidad disponible semanal que no se está utilizando en sus tres departamentos así: 200 horas en corte, 240 horas en soldadura y 150 horas en empaque. Producción propone que dicha capacidad sea utilizada en la producción de puertas, ventanas y claraboyas en la forma más eficiente posible, para dichos artículos se ha establecido los siguientes precios de venta $5000, $3000 y $4000 por unidad respectivamente. Además se ha determinado que para producir una puerta se requiere dos horas en corte, 3 horas en soldadura y 5 horas en empaque. Para producir una ventana se requiere 5 horas en corte, 4 horas en soldadura y 1 hora en empaque, maientras que para producir una claraboya se requiere 4 horas en corte, 2 horas en soldadura y 3 horas en empaque. Plantee el modelo se programación lineal que se genera si se sabe que mercadeo informo que mínimo se venderán 20 ventanas y como máximo 10 claraboyas.
Formulación de problemas de programación lineal: Ejercicio 3#
Para una cafetería que trabaja 24 horas se requieren las siguientes meseras:

Cada mesera trabaja 8 horas consecutivas por día. El administrador de la cafetería debe determinar el numero mínimo de meseras para cumplir los requisitos anteriores.
