Interpolación de lagrange

Esta es una técnica para obtener funciones polinómicas que se ajusten a un conjunto de puntos en coordenadas rectangulares.

La función polinómica se define como:

\[P_n (x) = ∑_{i=0}^{n-1} f(x_i)L_i(x)\]

Donde \(L_i(x)\) tiene la forma:

\[L_i(x) = 𝜫_{j=0; j \ne i}^{n-1} \frac{x - x_j}{xi - x_j}\]

con:

\(i= 0,1,...,n-1\)

\(j = 0,1,...,n-1\)

Ejemplo:

Encuentre una función polinómica que conecte los puntos:

x	y
0	1
1	3
2	0

Como solo tenemos 3 puntos de datos, entonces \(n=3\) y \(i = j = 0,1,2 \)

De igual forma asumimos:

\(x_0 = 0\) ; \(f(x_0)=1\)

\(x_1 = 1\) ; \(f(x_1)=3\)

\(x_2 = 2\) ; \(f(x_2)=0\)

x_values = [0, 1, 2]
y_values = [1, 3, 0]

# Veamos los datos
import matplotlib.pyplot as plt
fig, ax = plt.subplots()

ax.scatter(x_values,y_values, label="data")

ax.set_title("Interpolación de Lagrange")
ax.legend()
plt.show()

Primera iteración

\(i=0\)

\(j ̸= i\)

\[L_0(x) = \frac{x-x_1}{x_0 - x_1} * \frac{x-x_2}{x_0 - x_2}\]

from sympy import expand
x = symbols('x')
L0 = (x - x_values[1])/(x_values[0] - x_values[1]) * (x - x_values[2])/(x_values[0] - x_values[2])
expand(L0)

\[\displaystyle \frac{x^{2}}{2} - \frac{3 x}{2} + 1\]

Segunda iteración

\(i=1\)

\(j ̸= i\)

\[L_1(x) = \frac{x-x_0}{x_1 - x_0} * \frac{x-x_2}{x_1 - x_2}\]

x = symbols('x')
L1 = (x - x_values[0])/(x_values[1] - x_values[0]) * (x - x_values[2])/(x_values[1] - x_values[2])
expand(L1)

\[\displaystyle - x^{2} + 2 x\]

Tercera iteración

\(i=1\)

\(j ̸= i\)

\[L_2(x) = \frac{x-x_0}{x_2 - x_0} * \frac{x-x_1}{x_2 - x_1}\]

x = symbols('x')
L2 = (x - x_values[0])/(x_values[2] - x_values[0]) * (x - x_values[1])/(x_values[2] - x_values[1])
expand(L2)

\[\displaystyle \frac{x^{2}}{2} - \frac{x}{2}\]

Ahora calculemos la expresión final

\[P(x) = f(x_0)L_0(x) + f(x_1)L_1(x) + f(x_2)L_2(x)\]

Px = y_values[0]*L0 + y_values[1]*L1 + y_values[2]*L2
expand(Px)

\[\displaystyle - \frac{5 x^{2}}{2} + \frac{9 x}{2} + 1\]

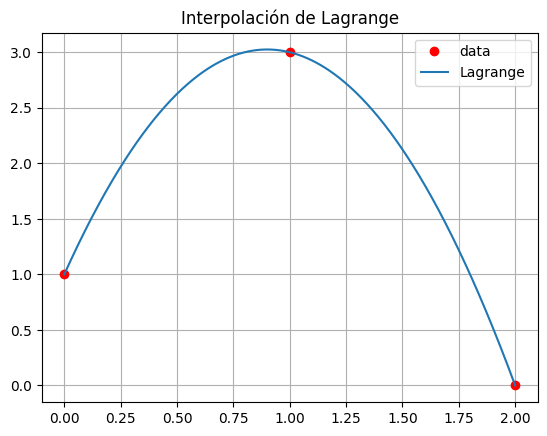
Evaluamos el polinomio resultante en los puntos \(x\)

plt.figure()
x_linspace = np.linspace(min(x_values), max(x_values), 400)
y_linspace = [Px.evalf(subs={x: val}) for val in x_linspace]

# Graficando los datos originales y el polinomio interpolado
plt.plot(x_values, y_values, 'ro', label='data')
plt.plot(x_linspace, y_linspace, label='Lagrange')
plt.title('Interpolación de Lagrange')
plt.grid(True)
plt.legend()
plt.grid(True)
plt.show()

✏️📘 Actividad en clase:

Deduzca e implemente el algoritmo para la interpolación de lagrange, automatice el procedimiento dado un archivo .csv con los valores a medir. Genere las gráficas y una tabla donde muestre los valores de \(x\), \(y\) y P(x). Finalmente imprima como queda el polinomio que interpola los datos.

#Tu código va aquí

#Tu código termina aquí

El polinomio de interpolación de Lagrange es:  -5*x**2/2 + 9*x/2 + 1

	x	y
0	0	1
1	1	3
2	2	0

\[\displaystyle - \frac{5 x^{2}}{2} + \frac{9 x}{2} + 1\]

Ejercicio:

La viscosidad dinámica del agua se relaciona con la temperatura T de la siguiente manera:

import pandas as pd

data = pd.DataFrame({'T [ºC]':[0,5,10,20,30,45], 'Viscosidad':[1.787,1.519,1.307,1.002,0.796,0.653]})
data.head()

	T [ºC]	Viscosidad
0	0	1.787
1	5	1.519
2	10	1.307
3	20	1.002
4	30	0.796

1. Utilice interpolación de lagrange diseñada en la actividad anterior para estimar un polinomio que represente la evolución de la viscosidad en función de la temperatura.

2. Calcule la viscosidad a una temperatura de \(15°C\)

## Acá empieza tu solución


## Acá termina tu solución

📘 Tarea

Investigue e implemente los siguientes algoritmos, describa su funcionamiento, el algoritmo y un ejemplo del funcionamiento

1. Splines Cúbicos.

2. Regresión Polinomial.