Regla de Simpson \(1/3\)

Esta regla no ajusta la curva a integrar por medio de una recta sino por una interpolación polinomial de segundo orden.

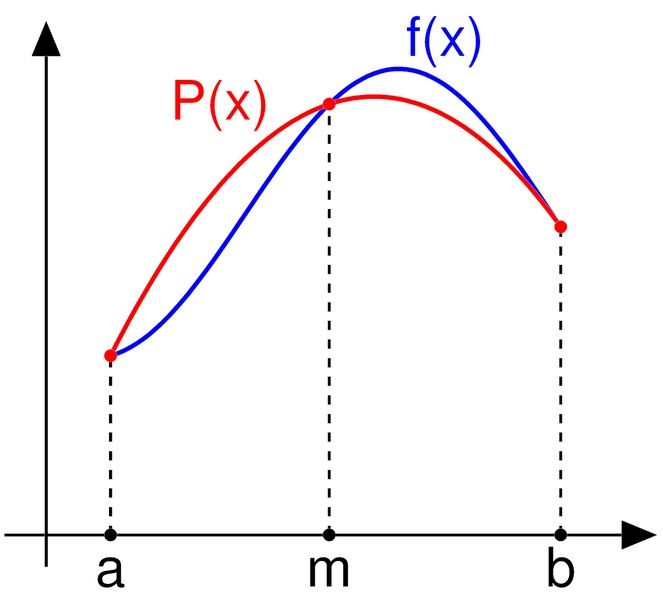
Como se muestra en el diagrama anterior, el integrando \(f(x)\) es aproximado por un polinomio de segundo orden, el interpolante cuadrático es \(P(x)\).

Sigue la aproximación para \(I\) ,

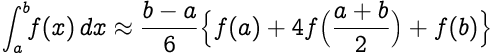
Reemplazando \(\frac{(b-a)}{2}\) como \(h\) , obtenemos \(I\) como: ,

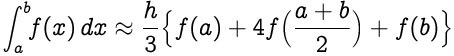
Como puedes ver, hay un factor de \(\frac{1}{3}\) en la expresión anterior. Por eso, se llama la Regla de \(\frac{1}{3}\) de Simpson.

Error absoluto

\[ e_{absoluto} = |\frac{I_{real} - I_{aprox}}{I_{real}}| \]

Algoritmo de regla simpson 1/3 para la integración

1. Calcular \(I\)

2. Calcular el \(e_{absoluto}\)

Ejercicio:

Integrar $\(\int_{a=1}^{b=2} x^2 dx \)$

utilizando la regla de simpson \(\frac{1}{3}\)

# Definimos las condiciones del problema
import sympy as sp
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

a = 1
b = 2

m = (a+b)/2

x = sp.symbols('x')
fx = x**2

fa = fx.subs({x:a})
fb = fx.subs({x:b})
fm = fx.subs({x:m})
print(f"f(a) = {fa} \nf(b) = {fb} \nf(m) = {fm:.2f}")

f(a) = 1 
f(b) = 4 
f(m) = 2.25

# Aplicamos la regla de simpson 1/3

I = (b-a) * ((fa + 4*fm + fb)/6)
print("I = ",I, "U^2")

I =  2.33333333333333 U^2

Tomemos el I real del anterior notebook:

\[ \int^{x=2}_{x=1} x^2 dx \]

analiticamente:

\[ \int^{2}_{1} x^2 dx = \frac{x^3}{3} |_1^2 = [\frac{2^3}{3} - \frac{1^3}{3}] = [\frac{8}{3} - \frac{1}{3}] = \frac{7}{3} = 2.333 U^2 \]

# Ahora usemos la funcion de integracion simbólica de sympy

I_real = sp.integrate(fx,(x,a,b))
print("La integral por sympy es: ",I_real)

La integral por sympy es:  7/3

error = np.abs((I_real - I)/(I_real))*100
print(f"La integración tiene un error de {error:.2f}%")

La integración tiene un error de 0.00%

import numpy as np
import matplotlib.pyplot as plt
plt.figure()

x = np.linspace(0,3, 100)
y = x**2

fig, ax = plt.subplots()
ax.plot(x,y,color='blue',label="$X^2$")
ax.grid()

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(y),ymax=max(y),color='k')
ax.hlines(y=0,xmin=min(x),xmax=max(x),color='k')

## límites xl y xu
ax.vlines(x=a, ymin=0, ymax=fa, color='r', linestyle='--')
ax.vlines(x=b, ymin=0, ymax=fb, color='r', linestyle='--')

ax.fill([a,a,m,b,b],[0,fa,fm,fb,0], 'r', alpha=0.2)

plt.grid(True)
plt.legend()

# Mostrar gráfica
plt.show()

<Figure size 640x480 with 0 Axes>

🧑‍💻👩‍💻 Actividad

Implemente un programa que permita dinámicante calcular la integral por regla de simpson 1/3 para cualquier función y que permita modificar los límites de la integral, pinte la gráfica y el resultado del área bajo la curva en la imágen además del error.

# Tu código va acá

# Tu código hasta acá

📘 Tarea

1. Implemente la versión Multiple de simpson 1/3 muestre con el mismo ejemplo el error del método para diferentes valores de segmentos.

2. Investigue e implemente el método de simpson 3/8 tanto simple como múltiple y realice la prueba con la función abordada en clase.

# Tu código va acá

# Tu código hasta acá