Método de la secante#

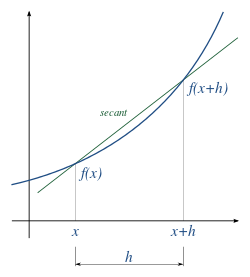
Este método es muy parecido a Newton Raphson,pero con la diferencia que no necesita evaluar en la derivada. Hay problemas en los que la derivada es dificil de calcular, el método de la secante permite resolver el problema ya que aproxima la raíz mediante rectas secantes.

Este método requiere dos puntos para poder empezar a iterar

Demostración del método#

\[f'(x) = \frac{f(x_i)-f(x_{i-1})}{x_i - x_{i-1}}\]

Recordemos de newton Raphson#

\[x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)} \]

Reemplacemos la aproximación de la derivada por la secante en la de newton raphson

\[x_{i+1} = x_i - \frac{f(x_i)}{\frac{f(x_i)-f(x_{i-1})}{x_i - x_{i-1}}}\]

despejando tenemos

\[x_{i+1} = x_i - \frac{f(x_i)[x_i - x_{i-1}]}{f(x_i)-f(x_{i-1})}\]

Algoritmo de la secante#

  1. Se calcula el siguiente \(x_{i+1}\) con la formula.

\[x_{i+1} = x_i - \frac{f(x_i)[x_i - x_{i-1}]}{f(x_i)-f(x_{i-1})}\]

  1. Se repite el paso 1 hasta convergencia.

Error relativo#

\[ e_r = \lvert \frac{x_{i+1}-x_{i}}{x_{i+1}}\rvert \]

Tolerancia#

Precisión que se requiere en el método!!

Actividad en clase: Iteremos hasta que el error sea de 1%#

Hallar la raíz de \(f(x)= e^{-x}-x\) usando el método de la secante con valores iniciales de \(x_{i-1}=0\) y \(x_i=1\); \(tol=1\%\)

Implemente el algoritmo usted mismo.#

## Tu código va acá

## Tu código termina acá

TAREA:#

  1. El método de la secante tiene una variación, llamada la secante modificada. Esta versión NO usa dos valores, sino un \(Δ\) muy pequeño para estimar la derivada.

\[f'(x) = \frac{f(x_i+Δx_i)-f(x_{i})}{Δx_i}\]

Reemplace y despeje el cálculo de \(x_{i+1}\) a partir de la ecuación anterior para implementar en un notebook el método de la secante modificada. Realice un ejemplo del método con gráficas, tabla de iteración y cálculo del error. Mencione las diferencias entre las dos versiones del método de la secante.

  1. Investigar el funcionamiento del método de iteración de punto fijo. Documentarlo en un notebook como lo ha visto para cada uno de los métodos vistos en clase. Debe tener en cuenta:

  • Funcionamiento gráfico

  • Demostración del método

  • Descripción del algoritmo (pasos)

  • Implementación paso a paso y completa del método

  • Ejemplo de funcionamiento del método. (gráficas, tabla de iteración, gráfico dinámico, etc)