Forma analítica de hallar los óptimos: en Sympy

De forma analítica, los óptimos de una función se pueden encontrar usando cálculo diferencial. Veamos como:

Pasos para encontrar óptimos de una función univariada \(f(x)\):

1. Primera Derivada: Calcula la \(f'(x)\) de la función.

import sympy as sp
import matplotlib.pyplot as plt
import numpy as np

# Definimos la variable y la función
x = sp.symbols('x')
f = x**3 - 6*x**2 + 4*x + 12

# Calculamos la primera derivada
f_prime = sp.diff(f, x)
f_prime

\[\displaystyle 3 x^{2} - 12 x + 4\]

2. Puntos Criticos: Encuentra los puntos críticos de la función resolviendo la ecuación \(f'(x)=0\). Estos puntos son candidatos a ser máximos o mínimos locales.

# Encuentra los puntos críticos resolviendo f'(x) = 0
critical_points = sp.solve(f_prime, x)
critical_points

[2 - 2*sqrt(6)/3, 2*sqrt(6)/3 + 2]

3. Segunda derivada (opcional pero útil): Calcula la segunda derivada \(f''(x)\). Esta derivada te puede ayudar a determinar la naturaleza de los puntos críticos:

• Si \(f''(x) > 0\) en un punto crítico \(x=c\), entonces \(f\) tiene un mínimo local en \(c\).

• Si \(f''(x) < 0\) en un punto crítico \(x=c\), entonces \(f\) tiene un máximo local en \(c\).

• Si \(f''(x) = 0\), la segunda derivada no es concluyente y se necesita otro método para determinar la naturaleza del punto.

# Calculamos la segunda derivada
f_double_prime = sp.diff(f_prime, x)
f_double_prime

\[\displaystyle 6 x - 12\]

# Determinamos la naturaleza de los puntos críticos
nature_of_critical_points = []
for point in critical_points:
    if f_double_prime.subs(x, point) > 0:
        nature = "mínimo"
    elif f_double_prime.subs(x, point) < 0:
        nature = "máximo"
    else:
        nature = "inconclusivo"
    nature_of_critical_points.append(nature)

print(critical_points)
print(nature_of_critical_points)

[2 - 2*sqrt(6)/3, 2*sqrt(6)/3 + 2]
['máximo', 'mínimo']

# Graficamos la función y los puntos críticos
f_lambda = sp.lambdify(x, f, "numpy")
x_vals = np.linspace(float(min(critical_points)) - 2, float(max(critical_points)) + 2, 400)
y_vals = f_lambda(x_vals)

plt.figure(figsize=(10, 6))
plt.plot(x_vals, y_vals, label=str(f), color='blue')
for point, nature in zip(critical_points, nature_of_critical_points):
    plt.scatter(point, f.subs(x, point), color='red')
    plt.text(point, f.subs(x, point), f'{point}: {nature}')

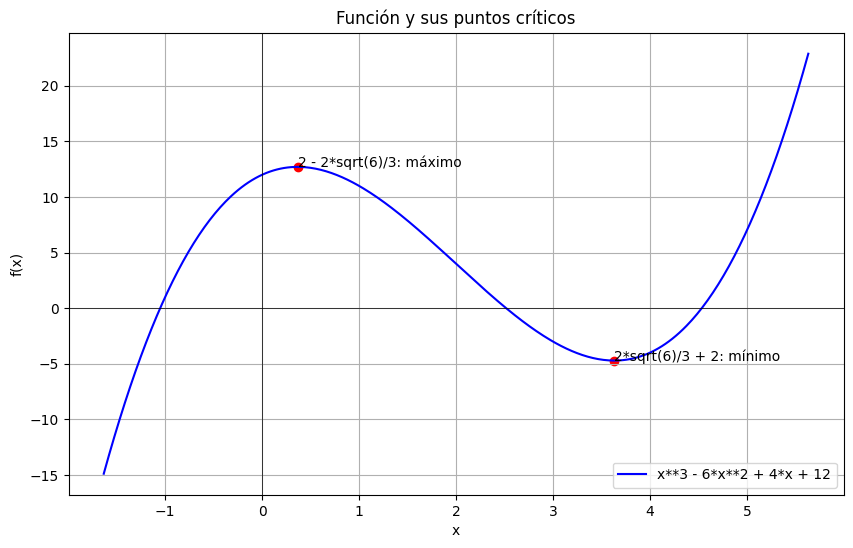
plt.title("Función y sus puntos críticos")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.legend()
plt.show()

Tarea

Realice en Sympy el código para realizar el análisis de optimización para funciones de N-variables.