Regla trapezoidal para integración numérica

En matemática la regla del trapecio es un método de integración numérica, es decir, un método para calcular aproximadamente el valor de la integral definida.

\[∫^b_a f(x)dx\]

La regla se basa en aproximar el valor de la integral de \(f(x)\) por el de la función lineal que pasa a través de los puntos \((a,f(a))\) y \((b,f(b))\)

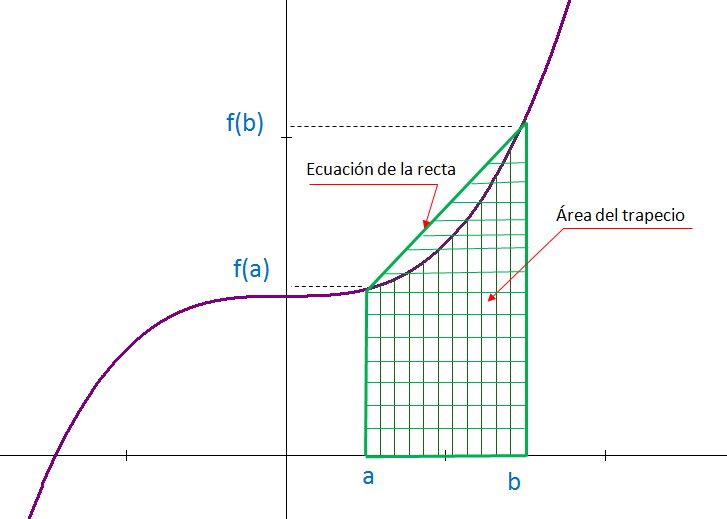
El objetivo de la regla es aproximar la integral a un polinomio de grado 1.

\[ I = ∫^b_a f(x)dx ≈ ∫^b_a f_1(x)dx \therefore F_1(x) \]

Se aproxima a una linea recta.

\[ y - y_1 = m(x - x_i) \]

Reemplazando con los valores de la imágen anterior…

\[ y - f(a) = \frac{f(b) - f(a)}{b - a} (x - a) \]

\[ y = f(a) + \frac{f(b) - f(a)}{b - a} (x - a) = f_1(x) \]

Entonces regresando la integración

\[ I = ∫^a_b [f(a) + \frac{f(b) - f(a)}{b - a}(x - a)] dx \]

Después de integrar tenemos la Regla trapezoidal

\[ I = (b-a) \frac{f(a)+f(b)}{2} \]

Donde:

\(I=\) área del trapecio

\((b - a) =\) ancho del trapecio

\(\frac{f(a)+f(b)}{2} = \) altura promedio

Error absoluto

\[ e_{absoluto} = |\frac{I_{real} - I_{aprox}}{I_{real}}| \]

Algoritmo de regla del trapecio para la integración

1. Calcular \(I\)

2. Calcular el \(e_{absoluto}\)

Ejercicio:

Integrar la siguiente función:

\[ \int^{x=2}_{x=1} x^2 dx \]

analiticamente:

\[ \int^{2}_{1} x^2 dx = \frac{x^3}{3} |_1^2 = [\frac{2^3}{3} - \frac{1^3}{3}] = [\frac{8}{3} - \frac{1}{3}] = \frac{7}{3} = 2.333 U^2 \]

# Definimos las condiciones del problema
import sympy as sp
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

a = 1
b = 2

x = sp.symbols('x')
fx = x**2

fa = fx.subs({x:a})
fb = fx.subs({x:b})

print(f"f(a) = {fa} \nf(b) = {fb}")

f(a) = 1 
f(b) = 4

# Aplicamos la regla trapezoidal

I = (b-a) * ((fa+fb)/2)
print("I = ",I, "U^2")

I =  5/2 U^2

# Calculemos el error

e = np.abs((2.333 - I)/(2.333)) * 100

print(f"El error es de {round(e,2)}%")

El error es de 7.16%

import numpy as np
import matplotlib.pyplot as plt
plt.figure()

x = np.linspace(0,3, 100)
y = x**2

fig, ax = plt.subplots()
ax.plot(x,y,color='blue',label="$X^2$")
ax.grid()

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(y),ymax=max(y),color='k')
ax.hlines(y=0,xmin=min(x),xmax=max(x),color='k')

## límites xl y xu
ax.vlines(x=a, ymin=0, ymax=fa, color='r', linestyle='--')
ax.vlines(x=b, ymin=0, ymax=fb, color='r', linestyle='--')
ax.plot([a,b],[fa,fb], color='r', linestyle='--')


ax.fill([a,a,b,b],[0,fa,fb,0], 'r', alpha=0.2)

plt.grid(True)
plt.legend()

# Mostrar gráfica
plt.show()

<Figure size 640x480 with 0 Axes>

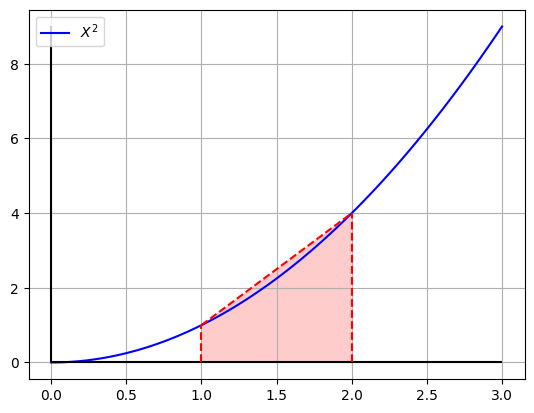
Actividad

Implemente un programa que permita dinámicante calcular la integral por regla del trapecio para cualquier función y que permita modificar los límites de la integral, pinte la gráfica y el resultado del área bajo la curva en la imágen además del error.

# Tu código va acá

# Tu código hasta acá