Unidad 3: Ajuste de Curvas e Interpolación#
Contenido de la unidad#

Ajuste de curvas e interpolación#
El ajuste de curvas y la interpolación son herramientas fundamentales en el análisis numérico y tienen amplias aplicaciones en la ciencia, la ingeniería y las finanzas. Estos métodos permiten modelar datos experimentales, estimar valores dentro o fuera de un conjunto de datos y representar funciones complicadas de manera simplificada.
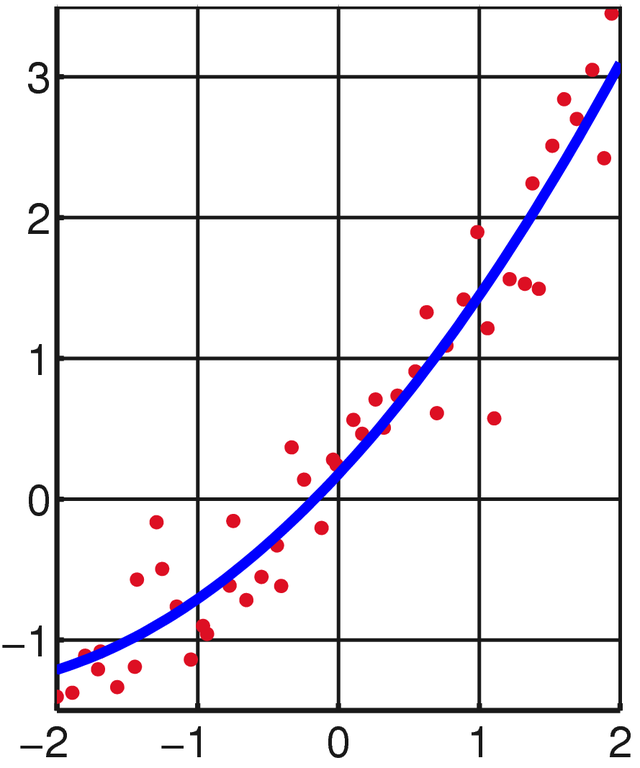
Ajuste de curvas#

El ajuste de curvas tiene como objetivo encontrar una función (por lo general una curva) que se aproxime lo mejor posible a un conjunto de datos. Dentro de las aplicaciones tenemos: Estimar tendencias de datos, modelar relaciones entre variables y predecir valores futuros.
El método más común es el de mínimos cuadrados, que minimiza la suma de los cuadrados de las diferencias entre los valores observados y los valores estimados por la curva.
Interpolación#
La interpolación tiene como objetivo estimar valores dentro de un intervalo a partir de un conjunto de puntos conocidos. Dentro de las aplicaciones tenemos: Estimar valores no conocidos en tablas, mejorar la resolución de imágenes y resolver ecuaciones diferenciales numéricamente.
El método más común es el de interpolación polinomial, que consiste en encontrar un polinomio que pase por todos los puntos conocidos. (por ejemplo interpolación de Lagrange).
Ajuste Vs Interpolación#
Mientras que la interpolación busca una función que pase exactamente por todos los puntos dados, el ajuste de curvas busca una función que se aproxime a los puntos pero no necesariamente los atraviese todos. Esto es especialmente útil cuando los datos tienen algún grado de error o ruido.