Método de la Falsa Posición

# @title Método de Falsa Posición
import numpy as np
import matplotlib.pyplot as plt
plt.figure()

x = np.linspace(-1.5,3.6, 100)
a = 0.5  # Desplazamiento hacia arriba
b = 0.5  # Desplazamiento hacia la derecha
y = np.cos(x+b)+a

fig, ax = plt.subplots()
ax.plot(x,y,color='blue',label="$cos(x/2) + 1/2$")
ax.grid()

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(y),ymax=max(y),color='k')
ax.hlines(y=0,xmin=min(x),xmax=max(x),color='k')


# Encontrar la posición del valor mínimo de y
indice_minimo = np.argmin(y)
posicion_minimo = x[indice_minimo]

# Encontrar la posición del valor máximo de y
indice_maximo = np.argmax(y)
posicion_maximo = x[indice_maximo]

## límites xl y xu
ax.vlines(x=posicion_maximo, ymin=0, ymax=max(y), color='k', linestyle='--',label='$x_l$')
ax.vlines(x=posicion_minimo, ymin=0, ymax=min(y), color='k', linestyle='-.',label='$x_u$')

## Trazo de la linea recta
ax.plot([posicion_maximo,posicion_minimo],[max(y),min(y)],color='red')
ax.plot([1.83],[0],marker='o',color='red',label='$x_r$')
"""
# Agregar texto en una ubicación específica
text_x = 0.6  # Posición en el eje X
text_y = 0  # Posición en el eje Y
ax.text(text_x, text_y+0.01, 'xu', fontsize=12, color='black')
ax.text(-text_x, -1*(text_y+0.03), 'xl', fontsize=12, color='black')"""

ax.set_title("$cos(x/2) + 1/2$")
plt.legend()
plt.show()

<Figure size 640x480 with 0 Axes>

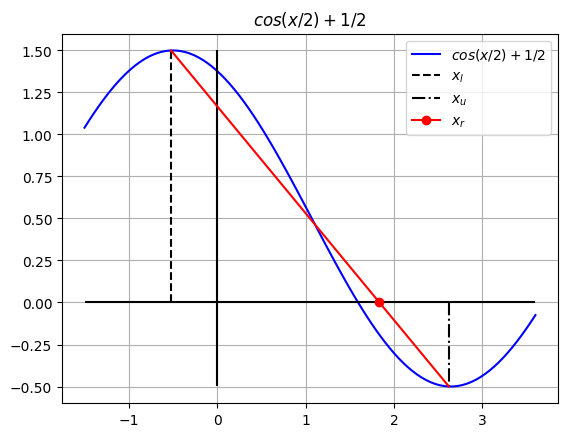
Consiste en hallar una raíz aproximada de una función en un intervalo dado, en algunos casos más eficiente que la bisección.

Toma en cuenta la magnitud de la función. Crea una linea recta entre los 2 puntos y la raíz de la recta se aproxima a la raíz de la función a diferencia de la bisección que parte en 2 lados iguales.

Teorema de la semejanza

\[\frac{f(x_l)}{x_r - x_l} = \frac{-f(x_u)}{x_r-x_u}\]

\[\frac{f(x_l)}{x_r - x_l} = \frac{f(x_u)}{x_u-x_r}\]

\[f(x_l)[x_r - x_u] = f(x_u)[x_r - x_l]\]

\[f(x_l)*x_r - f(x_l)*x_u = f(x_u)*x_r - f(x_u)*x_l\]

\[f(x_l)*x_r - f(x_u)*x_r = f(x_l)*x_u - f(x_u)*x_l\]

\[ x_r = \frac{f(x_l)*x_u - f(x_u)*x_l}{f(x_l)-f(x_u)}\]

Forma alternativa

\[x_r = \frac{f(x_l)*x_u}{f(x_l)-f(x_u)} - \frac{f(x_u)*x_l}{f(x_l)-f(x_u)}\]

\[x_r = x_u+ \frac{f(x_l)*x_u}{f(x_l)-f(x_u)} - \frac{f(x_u)*x_l}{f(x_l)-f(x_u)} - x_u\]

\[x_r = x_u - \frac{f(x_u)[x_l - x_u]}{f(x_l)-f(x_u)} \]

Esta última forma la necesitamos más adelante

Algoritmo para la Falsa posición

1. Encontrar un intervalo en donde $\(f(x1)*f(xu)<0\)$.

2. Se haya una raíz aproximada: $\( x_r = \frac{f(x_l)*x_u - f(x_u)*x_l}{f(x_l)-f(x_u)}\)$

3. Encontrar el subintervalo en donde cae la raíz de la siguiente forma:

• Si $\(f(xl)*f(xr) < 0\)\( la raíz está entre el intervalo \)xl\( y \)xr\(. Por tal razón, \)xu=xr$ y retorno al paso 2.

• Si $\(f(xl)*f(xr) > 0\)\( la raíz está entre el intervalo \)xr\( y \)xu\(. Por tal razón, \)xl=xr$ y retorno al paso 2.

• Si $\(f(xl)*f(xr) = 0\)\( la raíz es \)xr$ y termina el cálculo

Cálculo del error relativo

\[ e_r = \lvert \frac{xr_{actual}-xr_{anterior}}{xr_{actual}}\rvert \]

Tolerancia

Es qué tan aproximada será la raíz calculada.

Ejemplo

Calcular la raíz de \(f(x)=x^{3}-x\) en el intervalo (0.2, 1.7) con una tolerancia de 1%

Solución

import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

# Tomamos el intérvalo inicial y grafiquemos la función dentro de ese valor

x = sp.symbols('x')

y = x**3 - x
print("La función es: ",y)

xl,xu = (0.2,1.7)

print(f"El intervalo es: ({xl},{xu}) ")

fxl, fxu = (round(y.subs({x: xl}), 4), round(y.subs({x: xu}), 4))
print(f"la función evaluada en xl y xu respectivamente : (f({xl})={fxl},  f({xu})={fxu}) ")

La función es:  x**3 - x
El intervalo es: (0.2,1.7) 
la función evaluada en xl y xu respectivamente : (f(0.2)=-0.1920,  f(1.7)=3.2130) 

# @title Gráfica incial de la función en el rango especificado
import numpy as np
plt.figure()

r = np.linspace(0.1,2, 100)
fx = [y.subs({x:xi}) for xi in r]

fig, ax = plt.subplots()
ax.plot(r,fx,color='blue',label="$X^3 - X$")

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(fx)-0.5,ymax=max(fx)+0.5,color='k')
ax.hlines(y=0,xmin=min(r)-0.5,xmax=max(r)+0.5,color='k')

## Límites xl y xu
ax.vlines(x=xl, ymin=0, ymax=fxl, color='k', linestyle='--')
ax.vlines(x=xu, ymin=0, ymax=fxu, color='k', linestyle='--')

## Texto de xl y xu
ax.text(xl-0.02, 0.05, f'$x_l={xl}$', fontsize=11, color='black')
ax.text(xu+0.02, 0.05, f'$x_u={xu}$', fontsize=11, color='black')

ax.set_title("$X^3-X$")
ax.grid()
ax.legend()
plt.show()

<Figure size 640x480 with 0 Axes>

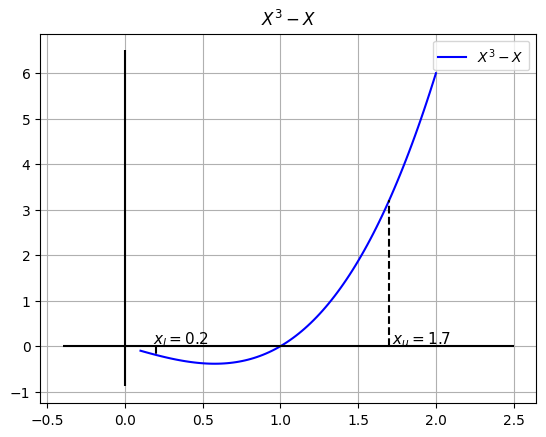
Calculemos ahora la raíz supuesta…

\[ x_r = \frac{f(x_l)*x_u - f(x_u)*x_l}{f(x_l)-f(x_u)}\]

xr = round(((fxl*xu)-(fxu*xl))/(fxl-fxu),4)
fxr = round(y.subs({x:xr}),4)
print(" xr = {:.4f}, f(xr) = {:.4f}".format(xr,fxr))

 xr = 0.2846, f(xr) = -0.2616

# @title Gráfica incial con el punto de $x_r$
import numpy as np
plt.figure()

r = np.linspace(0.1,2, 100)
fx = [y.subs({x:xi}) for xi in r]

fig, ax = plt.subplots()
ax.plot(r,fx,color='blue',label="$X^3 - X$")

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(fx)-0.5,ymax=max(fx)+0.5,color='k')
ax.hlines(y=0,xmin=min(r)-0.5,xmax=max(r)+0.5,color='k')

## Límites xl y xu
ax.vlines(x=xl, ymin=0, ymax=fxl, color='k', linestyle='--',label="$x_l =$ "+str(xl))
ax.vlines(x=xu, ymin=0, ymax=fxu, color='k', linestyle='-.',label="$x_u =$ "+str(xu))

## Texto de xl y xu
ax.text(xl-0.12, 0.05, f'$x_l$', fontsize=11, color='black')
ax.text(xu+0.02, 0.05, f'$x_u$', fontsize=11, color='black')


## Trazo de la linea recta
ax.plot([xl,xu],[fxl,fxu],color='red')

## Pintamos el punto intermedio
ax.plot(xr,0,color='red',label='Raíz',marker='o')
ax.text(xr,0.18, f'$x_r={xr}$', fontsize=11, color='black')

ax.set_title("$X^3-X$")
ax.grid()
ax.legend()
plt.show()

<Figure size 640x480 with 0 Axes>

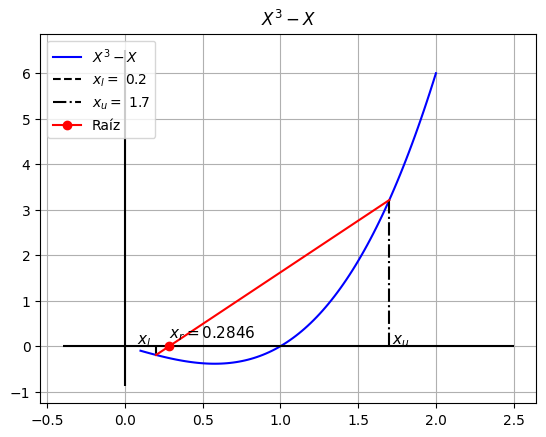
Calculemos el error…

Como es la primer iteración, NO tendremos forma de calcular un error ya que no existe un \(xr\) anterior. Para las siguientes iteraciones si vamos a calcular el error tomando la siguiente formula.

\[ e_r = \lvert \frac{Xr_{actual}-Xr_{anterior}}{Xr_{actual}}\rvert = INDIFERENTE \]

OJO: Solo para la primer iteración se define arbitrariamente

# @title Tabla de iteraciones
import pandas as pd

columnas = ['Xl','Xu','Xr','er(%)','f(Xl)','f(Xu)','f(Xr)']

primer_iter = {'Xl':[xl],'Xu':[xu],'Xr':[xr],'er(%)':[None],'f(Xl)':[fxl],'f(Xu)':[fxu],'f(Xr)':[fxr]}

tabla = pd.DataFrame(data=primer_iter,columns=columnas)
tabla.head(1)

	Xl	Xu	Xr	er(%)	f(Xl)	f(Xu)	f(Xr)
0	0.2	1.7	0.2846	None	-0.1920	3.2130	-0.2616

Revisemos las condiciones

• Si $\(f(xl)*f(xr) < 0\)$ la raíz está entre el intervalo xl y xr. Por tal razón, xu=xr y retorno al paso 2.

• Si $\(f(xl)*f(xr) > 0\)$ la raíz está entre el intervalo xr y xu. Por tal razón, xl=xr y retorno al paso 2.

• Si $\(f(xl)*f(xr) = 0\)$ la raíz es xr y termina el cálculo

if (fxl * fxr) < 0:
  print("La raíz está entre el intervalo xl y xr")
  xu = xr
elif (fxl*fxr) > 0:
  print("La raíz está entre el intervalo xr y xu")
  xl = xr
elif (fxl*fxr) == 0:
  print("terminé")

La raíz está entre el intervalo xr y xu

Repetimos los pasos anteriores para calcular el nuevo Xr y el error

fxl= round(y.subs({x:xl}),4)
fxu= round(y.subs({x:xu}),4)
xr2 = round(((fxl*xu)-(fxu*xl))/(fxl-fxu),4)
fxr2 = round(y.subs({x:xr2}),4)
print(" xr = {:.4f}, f(xr) = {:.4f}".format(xr2,fxr2))
error = round(np.abs((xr2-xr)/(xr2))*100,4)
print("El error de este cálculo es: {:.4f}% ".format(error))

 xr = 0.3912, f(xr) = -0.3313
El error de este cálculo es: 27.2500% 

# @title Gráfica del método para la iteración 2
import numpy as np
plt.figure()

r = np.linspace(0.1,2, 100)
fx = [y.subs({x:xi}) for xi in r]

fig, ax = plt.subplots()
ax.plot(r,fx,color='blue',label="$X^3 - X$")

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(fx)-0.5,ymax=max(fx)+0.5,color='k')
ax.hlines(y=0,xmin=min(r)-0.5,xmax=max(r)+0.5,color='k')

## Límites xl y xu
ax.vlines(x=xl, ymin=0, ymax=fxl, color='k', linestyle='--',label="$x_l =$ "+str(xl))
ax.vlines(x=xu, ymin=0, ymax=fxu, color='k', linestyle='-.',label="$x_u =$ "+str(xu))

## Texto de xl y xu
ax.text(xl-0.02, 0.05, f'$x_l$', fontsize=11, color='black')
ax.text(xu+0.02, 0.05, f'$x_u$', fontsize=11, color='black')

## Pintamos el punto intermedio
ax.plot(xr2,0,color='red',label='Raíz',marker='o')
ax.text(xr2,-0.3, f'$x_r={xr2}$', fontsize=11, color='black')

## Trazo de la linea recta
ax.plot([xl,xu],[fxl,fxu],color='red')

ax.set_title("$X^3-X$")
ax.grid()
ax.legend()
plt.show()

<Figure size 640x480 with 0 Axes>

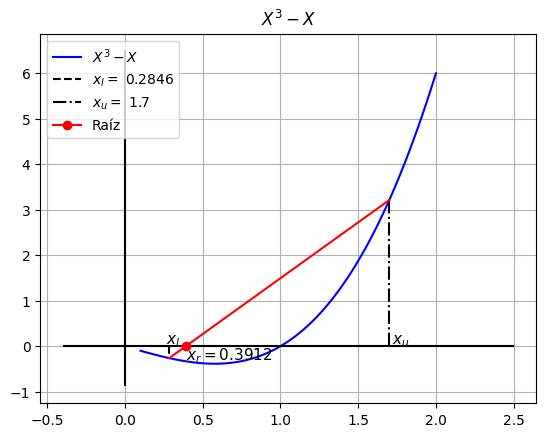
# @title Actualizamos la tabla de iteraciones
nueva_fila = {'Xl': xl, 'Xu': xu, 'Xr': xr2, 'er(%)': error, 'f(Xl)': fxl, 'f(Xu)': fxu, 'f(Xr)':fxr2}
tabla = tabla.append(nueva_fila, ignore_index=True)
tabla.head()

<ipython-input-74-912f58af88d4>:3: FutureWarning: The frame.append method is deprecated and will be removed from pandas in a future version. Use pandas.concat instead.
  tabla = tabla.append(nueva_fila, ignore_index=True)

	Xl	Xu	Xr	er(%)	f(Xl)	f(Xu)	f(Xr)
0	0.2	1.7	0.2846	None	-0.1920	3.2130	-0.2616
1	0.2846	1.7	0.3912	27.25	-0.2616	3.2130	-0.3313

Actividad en clase: Iteremos hasta que el error sea de 1%

Implemente el algoritmo usted mismo.

## Tu código va acá

## Tu código termina acá

Ejercicio

Calcular la raíz de \(y = \frac{667,38}{x}(1 - e^{-0,146843x}) - 40\) en el intervalo (12, 16) con una tolerancia de 0.5%

Implementar una función que me permita dinámicamente modificar la tolerancia y el intervalo, además de la gráfica y que me retorne la raíz, el error, la tabla de iteraciones y la gráfica dinámica de como itera el método.