Regla trapezoidal multiple

Regla trapezoidal multiple#

Mejora la regla trapezoidal con el fin de partir el intervalo de integración en varios segmentos y aplicar la regla trapezoidal varias veces para dar mayor precisión.

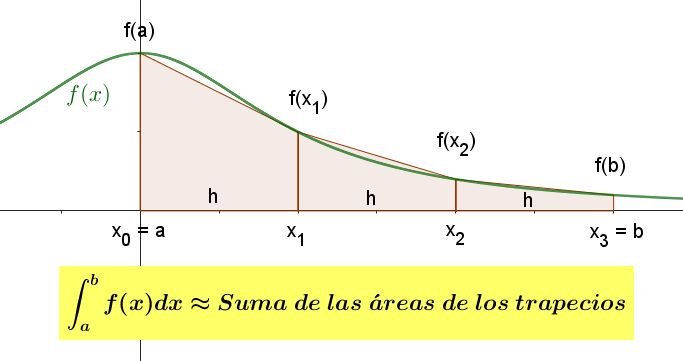
Donde

\[ h = \frac{b - a}{n} \]

$h =$ ancho del segmento

$n =$ número de segmentos deseados

$a = x_0$

$b = x_n$

Entonces la formula queda:

\[ I = \frac{h}{2} [f(x_0) + 2 ∑_{i=1}^{n-1} f(x_i) + f(x_n)] \]

que se traduce en:

\[ I = (b-a) [\frac{f(x_0) + 2 ∑_{i=1}^{n-1} f(x_i) + f(x_n)}{2n}] \]

Error absoluto#

\[ e_{absoluto} = |\frac{I_{real} - I_{aprox}}{I_{real}}| \]

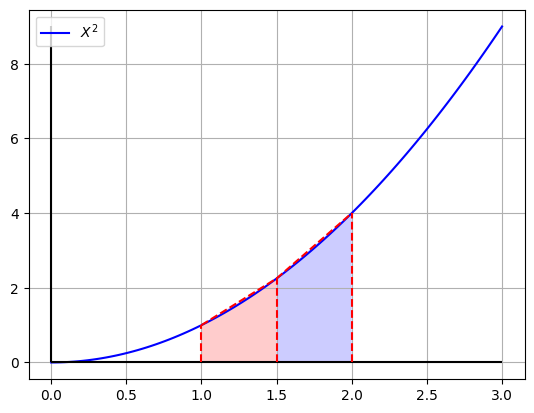
Ejercicio:#

Integrar $$\int_{a=1}^{b=2} x^2 dx $$

utilizando regla trapezoidal multiple con dos segmentos.

import sympy as sp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

a = 1
b = 2

n = 2
x = sp.symbols('x')
fx = x**2

h = (b - a) / n

print (f"f(x)= {fx}, a = {a}, b = {b}, n = {n}, h = {h}")

f(x)= x**2, a = 1, b = 2, n = 2, h = 0.5

t = np.arange(a,b+h,h)
y = [float(round(fx.subs({x:ti}),3)) for ti in t]

print("xi = ",t)
print("f(xi)= ",y)

xi =  [1.  1.5 2. ]
f(xi)=  [1.0, 2.25, 4.0]

I = h/2 * (y[0] + 2 * (y[1]) + y[-1])

Tomemos el I real del anterior notebook:#

\[ \int^{x=2}_{x=1} x^2 dx \]

analiticamente:

\[ \int^{2}_{1} x^2 dx = \frac{x^3}{3} |_1^2 = [\frac{2^3}{3} - \frac{1^3}{3}] = [\frac{8}{3} - \frac{1}{3}] = \frac{7}{3} = 2.333 U^2 \]

# Ahora usemos la funcion de integracion simbólica de sympy

I_real = sp.integrate(fx,(x,a,b))
print("La integral por sympy es: ",I_real)

La integral por sympy es:  7/3

error = np.abs((I_real - I)/(I_real))*100
print(f"La integración tiene un error de {error:.2f}%")

La integración tiene un error de 1.79%

import numpy as np
import matplotlib.pyplot as plt
plt.figure()

t = np.linspace(0,3, 100)
y = t**2

fig, ax = plt.subplots()
ax.plot(t,y,color='blue',label="$X^2$")
ax.grid()

fa = fx.subs({x:a})
fb = fx.subs({x:b})

## Plano cartesiano (Ejes)
ax.vlines(x=0,ymin=min(y),ymax=max(y),color='k')
ax.hlines(y=0,xmin=min(t),xmax=max(t),color='k')

## límites xl y xu
ax.vlines(x=a, ymin=0, ymax=fa, color='r', linestyle='--')
ax.vlines(x=b, ymin=0, ymax=fb, color='r', linestyle='--')

fa = fx.subs({x:a})
fb = fx.subs({x:a+h})
ax.vlines(x=a+h, ymin=0, ymax=fb, color='r', linestyle='--')

ax.fill([a,a,a+h,a+h],[0,fa,fb,0], 'r', alpha=0.2)
ax.plot([a,a+h],[fa,fb], color='r', linestyle='--')
fb = fx.subs({x:b})
ax.plot([a+h,b],[fx.subs({x:a+h}),fb], color='r', linestyle='--')
ax.fill([a+h,a+h,b,b],[0,fx.subs({x:a+h}),fb,0], 'b', alpha=0.2)
plt.grid(True)
plt.legend()

# Mostrar gráfica
plt.show()

<Figure size 640x480 with 0 Axes>

../../_images/0e93e2e73fa38bffe87664a924d21b533547a45d27c58f3d7662c4fa72d5bb51.png

Actividad#

Complete el algoritmo y genere un programa que generalice y que permita aplicar el método visto para diferentes valores de a, b, segmentos de trapecios (n). muestre el error del cálculo al finalizar.

Resuelve: