Método de euler para integración numérica

En matemática y computación, el método de Euler, llamado así en honor de Leonhard Euler, es un procedimiento de integración numérica para resolver ecuaciones diferenciales ordinarias a partir de un valor inicial dado.

El método de Euler es el más simpe de los métodos numéricos. útil para resolver PVI.

Problema de valores inciales (PVI)

\[PVI => \frac{dy}{dx} = f(x,y) ; y(x_0) = y_0 ; y(x_i) = ?\]

Consiste en dividir los intervalos que van desde \(x_0\) a \(x_f\) en \(n\) intervalos de ancho \(h\) de la forma:

\[h = \frac{x_f - x_0}{n}\]

De esta manera se obtiene un conjunto discreto de \(n+1\) puntos: \(x_0,x_1,x_2,x_3,...,x_n\) del intervalo de interés \([x_0 , x_f]\). Para cualquiera de estos puntos se cumple que:

\[x_i = x_0 + i * h\]

con: \(0 ≤ i ≤ n\)

La condición inicial \(y(x_0) = y_0\), representa el punto \(P_0 = (x_0, y_0)\) por donde pasa la curva solución de la ecuación del planteamiento inicial, la cual se denota como \(F(x) = y\)

Ya teniendo el punto \(P_0\) se puede evaluar la primera derivada de \(F(x)\) en ese punto, por lo tanto:

\[F'(x) = \frac{dy}{dx} ]_{P_0} = f'(x_0,y_0)\]

Con esta información se traza una recta, aquella que pasa por \(P_0\) y de pendiente \(f'(x_0, y_0)\). Esta recta aproxima a \(F(x)\) en una vecindad de \(x_0\)

Tóme la recta como reemplazo de \(F(x)\) y localice en la recta el valor de \(y\) correspondiente \(x_1\). Entonces, podemos deducir según la gráfica que:

\[\frac{y_1 - y_0}{x_1 - x_0} = f'(x_0,y_0)\]

Si se resuelve para \(y_1\)

\[y_1 = y_0 + (x_1 - x_0)f'(x_0,y_0) = y_0 +h f'(x_0,y_0)\]

El valor de la imágen puede iterarse de la siguiente forma:

\[y_1 = y_0 + hf'(x_0,y_0)\]

\[y_2 = y_1 + hf'(x_1,y_1)\]

\[…\]

\[y_{i+1} = y_i + hf'(x_i,y_i)\]

\[…\]

\[y_n = y_{n-1} + hf'(x_{n-1},y_{n-1})\]

Algoritmo de Euler para la integración

1. Hacer \(y_{i+1} = y_i + hf'(x_i,y_i)\)

2. Hacer \(x_{i} = x_{i+1}\)

Ejercicio:

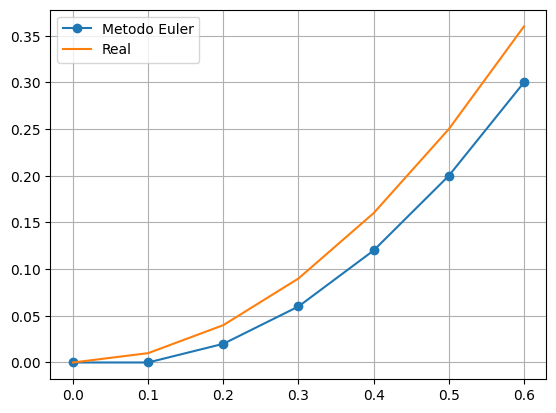
Hallar la integral geométrica de la función \(y' = 2t\) con una condicion incial y(0)=0 y un tiempo de integración de \(0\) hasta \(0.6\) y un paso de integración de \(0.1\)

# Definimos la función
import sympy as sp
import numpy as np
import pandas as pd

t = sp.symbols('t')
dy = 2*t

y0 = 0 # Condicion inicial
ti = 0 # Tiempo inicial
h = 0.1 # paso de integración
tf = 0.6 # Tiempo final

# Definimos los vectores donde almacenaremos el resultado.
x = np.arange(ti, tf + h, h)
y = np.empty_like(x)
y[0] = y0
print(x)
print(y)

[0.  0.1 0.2 0.3 0.4 0.5 0.6]
[ 0.00000000e+000  0.00000000e+000  2.73197970e-285  4.67514788e+180
 -3.32749444e-109  4.31912682e-239  5.79821152e-081]

columnas = ['it','t','yi','yi+1']
tabla = pd.DataFrame(columns=columnas)
for i in range(0,len(y)-1):
  y[i+1] = y[i] + h * dy.subs({t:x[i]})
  nueva_fila = pd.DataFrame(data={'it':[i+1],'t':[round(x[i],2)],'yi':[round(y[i],2)],"yi+1":[round(y[i+1],2)]})
  tabla = pd.concat([tabla,nueva_fila], ignore_index=True)

tabla.head()

	it	t	yi	yi+1
0	1	0.0	0.00	0.00
1	2	0.1	0.00	0.02
2	3	0.2	0.02	0.06
3	4	0.3	0.06	0.12
4	5	0.4	0.12	0.20

import matplotlib.pyplot as plt
plt.figure()
fig, ax = plt.subplots()
ax.grid()
ax.plot(x,y, marker='o', label ="Metodo Euler")
ax.plot(x, x**2, label="Real")
ax.legend()

<matplotlib.legend.Legend at 0x7eb7e312c940>

<Figure size 640x480 with 0 Axes>

Actividad

Realice un programa que permita visualizar de forma interactiva para cada iteración como cambia la gráfica de la integración, además que permita modificar de forma interactiva los pasos de integración, la derivada o las condiciones inciales.

a. Realice una prueba con \(y' = 3t^2\) desde -2 hasta 2 con paso 0.2

# Tu código va acá

# Tu código hasta acá