Unidad 2: Cálculo de raices#
Contenido de la unidad#

Solución de un problema matemático.#
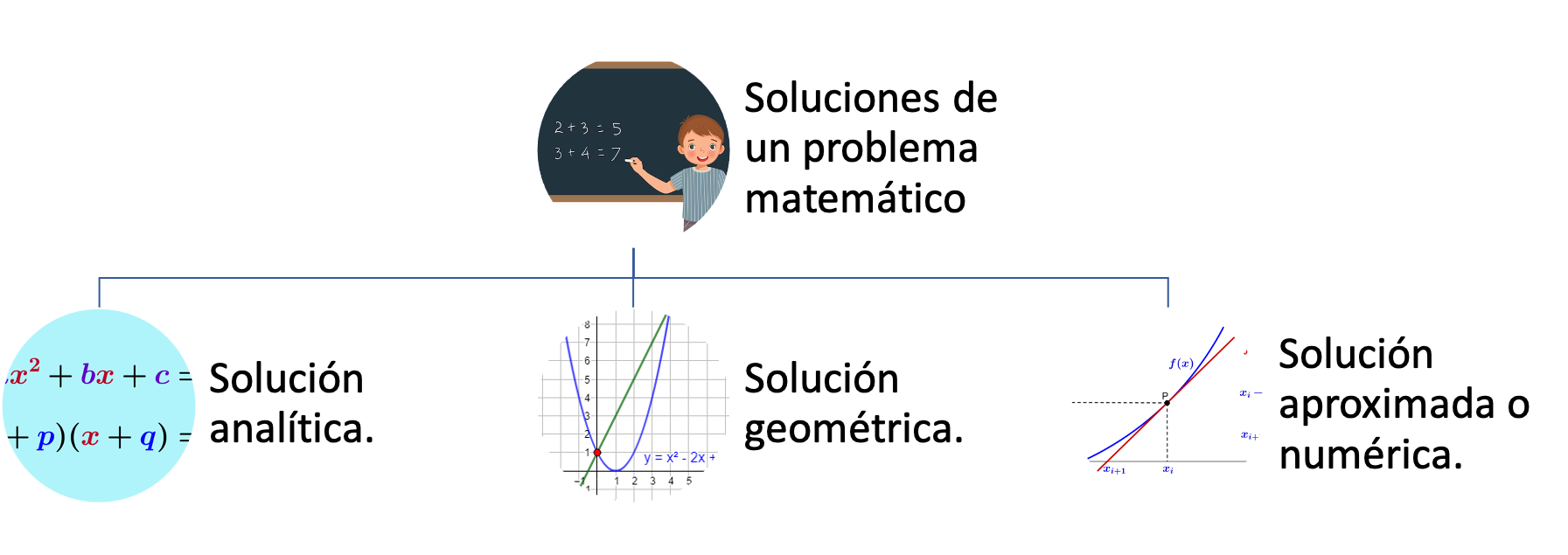
Raices de funciones#
Una raiz se define como una función igualada a cero o el intercepto de una curva con el eje X
\[
f(x) = 0
\]
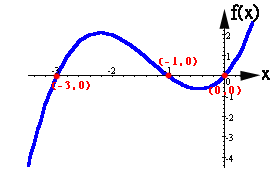
Encontremos las raices de la siguiente función…
Analiticamente ¿cuál es la solución?, ¿qué multiplicidad tiene la función?
\[
f(x) = x^2 + 5x + 6
\]
Encontremos las raices de la siguiente función…
Analiticamente ¿cuál es la solución?, ¿qué multiplicidad tiene la función?
\[
f(x) = x^2 + 2x + 1
\]
Métodos numéricos para hallar raices#
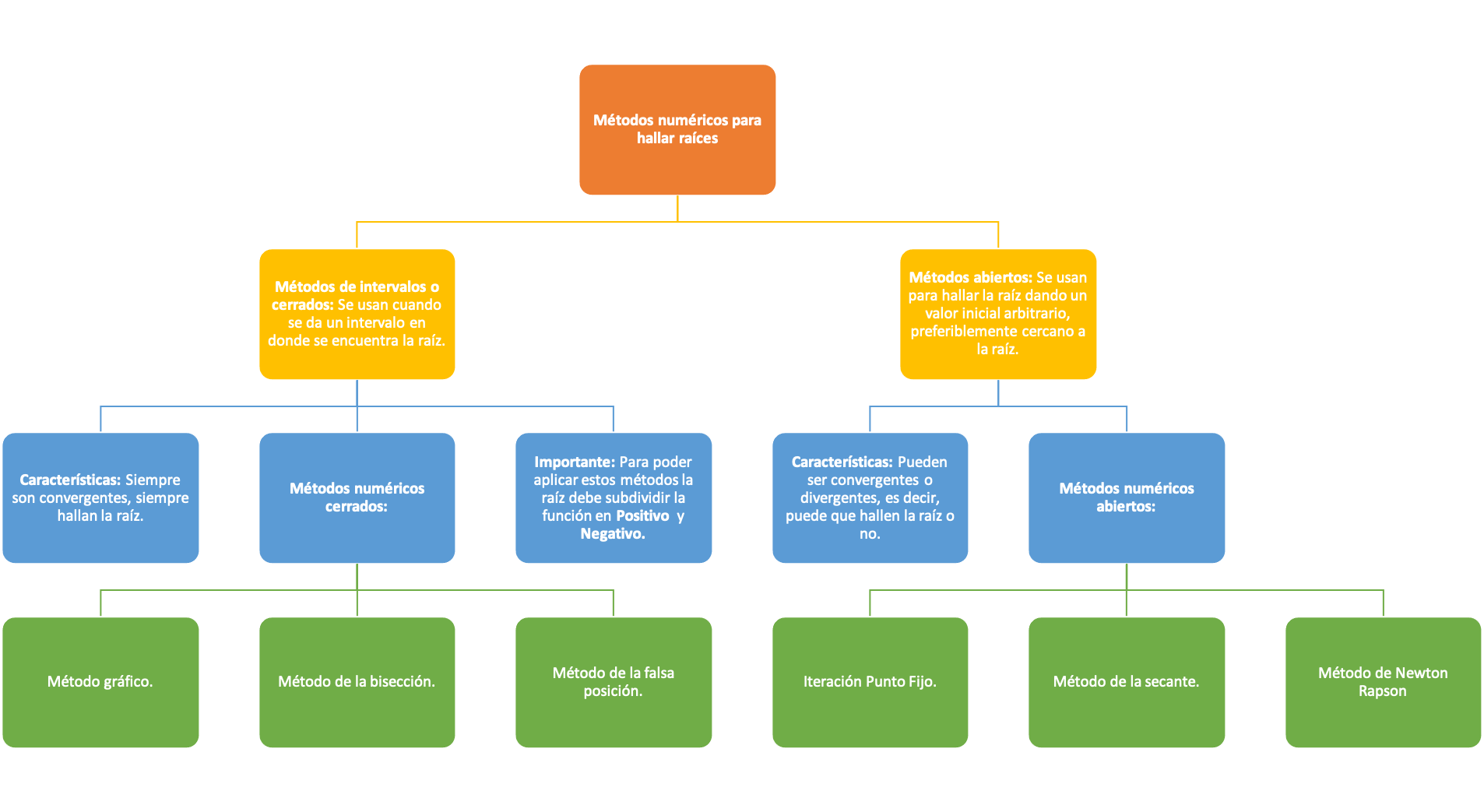
Método gráfico:#
El método gráfico sirve como método inicial para conocer dónde están las raices de forma aproximada.
Note
Hallar una raíz geométricamente consiste en hallar el punto de cruce con el eje X
Encontremos las raices de la siguiente función…
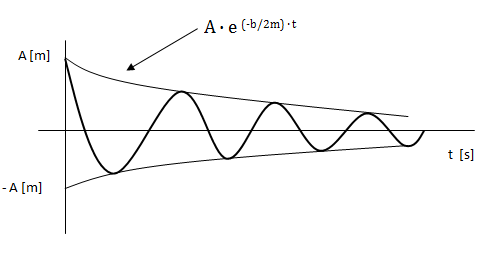
Este ejemplo tiene 8 raices de multiplicidad 1
📘 Ejercicio en clase#
