Matrices y vectores#
import numpy as np
A=np.array(['a','b','c','d','e'])
x='e'
i=0
q=True
n=len(A)
while q and (i!=n) :
q=not(A[i]==x)
i=i+1
if i==n and q==True:
print('No se encontró el elemento')
else:
print('la posición es:',i-1,'El valor es:',A[i-1])
la posición es: 4 El valor es: e
A=np.array(['a','b','c','d','e'])
x='e'
i=0
n=len(A)
while i!=n:
if A[i]==x:
break
i=i+1
if i==n:
print('No se encontró el elemento')
else:
print('la posición es:',i,'El valor es:',A[i])
la posición es: 4 El valor es: e
A=np.array(['a','b','c','d','e'])
x='c'
n=len(A)
A=np.append(A,x)
i=0
while not(A[i]==x):
i=i+1
if i==n:
print('No se encontró el elemento')
else:
print('la posición es:',i,'El valor es:',A[i])
la posición es: 2 El valor es: c
import numpy as np
A=np.array([2,3,5,6,8,10,11])
x=11
i=0
j=len(A)
q=True
while q and (i<=j):
k=(i+j)//2
if A[k]==x:
q=False
else:
if A[k]<x:
i=k+1
else:
j=k-1
if q==True:
print('No se encontró el elemento')
else:
print('la posición es:',k,'El valor es:',A[k])
la posición es: 6 El valor es: 11
v1=[1,2,3,4]
v2=[4,5,6,7]
n=len(v1)
s=0
i=0
while i!=n:
s=s+v1[i]*v2[i]
i+=1
print('el producto escalar es: ',s)
el producto escalar es: 60
v1=[1,2,3,4]
v2=[4,5,6,7]
n=len(v1)
s=0
i=0
for i in range(n):
s=s+v1[i]*v2[i]
print('el producto escalar es: ',s)
el producto escalar es: 60
A=[1,2,4,5,3,6,7]
j=0
k=0
for k in range(1,len(A)):
if A[k]>A[j]:
j=k
print('el elemento maximo es:',A[j], 'en la posición: ',j)
el elemento maximo es: 7 en la posición: 6
n=3
s=0
for x in range(1,n+1):
potencia=1
for i in range(1,x+1):
potencia=potencia*x
s=s+potencia
print('el resultado de la suma es: ',s)
el resultado de la suma es: 32
n=3
s=0
for x in range(1,n+1):
s=s+x**x
print('el resultado de la suma es: ',s)
el resultado de la suma es: 32
x=np.random.randint(200, size=100)
h=0
for h in range(len(x)):
j=h
for k in range(h+1,len(x)):
if x[k]>x[j]:
j=k
u=x[h]
x[h]=x[j]
x[j]=u
print(x)
[198 194 192 187 181 180 179 179 178 177 175 172 172 171 168 166 164 163
161 161 160 158 156 154 152 147 146 146 146 142 140 135 135 130 128 126
124 120 119 118 118 116 112 110 107 102 101 101 100 100 95 89 88 86
84 83 82 82 82 81 81 80 77 76 73 73 72 71 69 68 67 66
61 61 57 55 49 45 42 41 41 40 39 36 35 35 29 23 22 21
18 17 15 13 12 12 10 8 6 0]
Numpy#
Con la librería numpy se trabaja con matrices de forma natural. Fíjate cómo se declaran y cómo descubrimos sus dimensiones.
https://s3.amazonaws.com/assets.datacamp.com/blog_assets/Numpy_Python_Cheat_Sheet.pdf
import numpy as np
a = np.array([[1,2,3,4,5],
[5,4,3,2,1],
[9,8,7,6,5],
[7,6,5,6,7],
[2,2,2,3,3],
[4,3,4,3,4],
[5,1,1,4,1]]).astype('int32')
print(a, type(a),a.nbytes,"\n")
print("a shape", a.shape,"\n")
print("a rows", a.shape[0],"\n")
print("a cols", a.shape[1])
[[1 2 3 4 5]
[5 4 3 2 1]
[9 8 7 6 5]
[7 6 5 6 7]
[2 2 2 3 3]
[4 3 4 3 4]
[5 1 1 4 1]] <class 'numpy.ndarray'> 140
a shape (7, 5)
a rows 7
a cols 5
a[0,0]=100
a
array([[100, 2, 3, 4, 5],
[ 5, 4, 3, 2, 1],
[ 9, 8, 7, 6, 5],
[ 7, 6, 5, 6, 7],
[ 2, 2, 2, 3, 3],
[ 4, 3, 4, 3, 4],
[ 5, 1, 1, 4, 1]], dtype=int32)
a.nbytes
140
v = np.array([2,3,4,5,6,7,3,12])
print("v shape", v.shape)
print("v elems", v.shape[0])
print(v, type(v))
v shape (8,)
v elems 8
[ 2 3 4 5 6 7 3 12] <class 'numpy.ndarray'>
v[3:-1]
array([5, 6, 7, 3])
np.min(v), np.max(v)
(2, 12)
Con la notación de índices accedemos a columas o filas enteras, rangos de columnas o filas, elementos individuales o porciones de una matriz o un vector.
print("una fila " ,a[2])
print("una fila " ,a[2,:])
print("una columna " ,a[:,2])
print("un elemento " ,a[2,2])
print("varias filas \n",a[2:5])
print("varias columnas \n",a[:,1:3])
print("una porcion \n",a[2:5,1:3])
una fila [9 8 7 6 5]
una fila [9 8 7 6 5]
una columna [3 3 7 5 2 4 1]
un elemento 7
varias filas
[[9 8 7 6 5]
[7 6 5 6 7]
[2 2 2 3 3]]
varias columnas
[[2 3]
[4 3]
[8 7]
[6 5]
[2 2]
[3 4]
[1 1]]
una porcion
[[8 7]
[6 5]
[2 2]]
Muchas funciones de la librería numpy operan sobre una matriz completa, o de forma separada por columnas o filas según el valor del argumento axis.
print(a)
print("suma total", np.sum(a))
print("suma eje 0", np.sum(a, axis=0))
print("suma eje 1", np.sum(a, axis=1))
print("promedio total", np.mean(a))
print("promedio eje 0", np.mean(a, axis=0))
print("promedio eje 1", np.mean(a, axis=1))
[[100 2 3 4 5]
[ 5 4 3 2 1]
[ 9 8 7 6 5]
[ 7 6 5 6 7]
[ 2 2 2 3 3]
[ 4 3 4 3 4]
[ 5 1 1 4 1]]
suma total 237
suma eje 0 [132 26 25 28 26]
suma eje 1 [114 15 35 31 12 18 12]
promedio total 6.771428571428571
promedio eje 0 [18.85714286 3.71428571 3.57142857 4. 3.71428571]
promedio eje 1 [22.8 3. 7. 6.2 2.4 3.6 2.4]
Las matrices en Python pueden tener un número arbitrario de dimensiones y podemos acceder a submatrices en la dirección o dimensión que queramos.
z = np.random.randint(-20,20, size=(5,5))
print(z)
[[-19 4 -13 -19 13]
[ 19 6 -9 -9 -16]
[-11 12 -6 -20 16]
[ -4 -1 -4 13 0]
[-19 13 -1 9 8]]
np.sum(z, axis=1)
array([-34, -9, -9, 4, 10])
#m = np.random.randint(10, size=(3,3,3))
print("Matrix 3D completa\n", m)
print("----------\n", m[0,:,:])
print("----------\n", m[1,:,:])
print("----------\n", m[:,0,:])
print("----------\n", m[:,0,1])
print("----------\n", np.mean(m, axis=1))
Matrix 3D completa
[[[7 0 8]
[4 0 4]
[3 4 9]]
[[4 7 9]
[2 2 6]
[0 5 9]]
[[8 6 9]
[0 3 0]
[0 9 2]]]
----------
[[7 0 8]
[4 0 4]
[3 4 9]]
----------
[[4 7 9]
[2 2 6]
[0 5 9]]
----------
[[7 0 8]
[4 7 9]
[8 6 9]]
----------
[0 7 6]
----------
[[4.66666667 1.33333333 7. ]
[2. 4.66666667 8. ]
[2.66666667 6. 3.66666667]]
m.shape
(3, 3, 3)
m
Generación de matrices y vectores#
print("matrix identidad\n", np.eye(3))
print("vector de ceros", np.zeros(4))
print("matriz de ceros\n", np.zeros((3,2)))
print("matriz de unos\n", np.ones((2,3)))
print("vector rango", np.arange(10))
print("vector rango", np.arange(5,10))
print("vector espacio lineal", np.linspace(2,12,11))
print("matriz aleatoria según distribución uniforme [0,1]\n", np.random.random(size=(3,5)))
print("vector aleatorio de enteros entre 0 y 5", np.random.randint(5, size=10))
matrix identidad
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
vector de ceros [0. 0. 0. 0.]
matriz de ceros
[[0. 0.]
[0. 0.]
[0. 0.]]
matriz de unos
[[1. 1. 1.]
[1. 1. 1.]]
vector rango [0 1 2 3 4 5 6 7 8 9]
vector rango [5 6 7 8 9]
vector espacio lineal [ 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.]
matriz aleatoria según distribución uniforme [0,1]
[[0.57996022 0.65361661 0.99420518 0.12111156 0.26731741]
[0.206147 0.25575192 0.66588831 0.55022348 0.76820253]
[0.51384056 0.63172996 0.50836505 0.41256526 0.66835632]]
vector aleatorio de enteros entre 0 y 5 [0 3 3 0 3 3 2 1 2 1]
Operaciones vectorizadas#
import numpy as np
v = np.array([10,12,13,15,20])
print(v)
print(v+1)
print(v*2)
a = np.random.randint(100, size=5)
print(a)
print(v.dot(a))
[10 12 13 15 20]
[11 13 14 16 21]
[20 24 26 30 40]
[60 83 36 31 82]
4169
v1=np.array([2,-1,1])
v2=np.array([-3,1,1])
print(v1.dot(v2))
print(v1*v2)
print(np.cross(v2,v1))
print(np.cross(v1,v2).dot(v1))
print(np.cross(v1,v2).dot(v2))
-6
[-6 -1 1]
[2 5 1]
0
0
m1=np.array([[1,2],[3,4]])
m2=np.array([[4,8],[9,1]])
m1*m2
array([[ 4, 16],
[27, 4]])
m1.dot(m2)
array([[22, 10],
[48, 28]])
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[6,5,4],[3,2,1]])
c = np.array([[1,2],[4,5]])
print(a)
print("--")
print(a.T)
print("--")
print(b)
print("--")
print(a.T.dot(a))
print("--")
print(a*b)
print("--")
x=np.array([[2,3],[4,5]])
z=np.array([[5,6,7],[2,3,1]])
print(x.dot(z))
[[1 2 3]
[4 5 6]]
--
[[1 4]
[2 5]
[3 6]]
--
[[6 5 4]
[3 2 1]]
--
[[17 22 27]
[22 29 36]
[27 36 45]]
--
[[ 6 10 12]
[12 10 6]]
--
[[16 21 17]
[30 39 33]]
Las operaciones vectorizadas también funcionan con expresiones booleanas. Fíjate cómo se indexa un vector con una expresión booleana para seleccionar un conjunto de elementos.
a = np.array([1,8,4,10,-4,5])
print("posiciones en a >4:", a>4)
print("elementos de a >4:",a[a>4])
posiciones en a >4: [False True False True False True]
elementos de a >4: [ 8 10 5]
Más operaciones vectorizadas#
a = np.random.randint(100, size=(6,10))
a
array([[14, 19, 5, 87, 99, 92, 31, 63, 18, 44],
[81, 26, 65, 86, 2, 24, 99, 79, 71, 37],
[42, 87, 8, 92, 63, 29, 31, 85, 75, 93],
[59, 58, 97, 10, 12, 99, 86, 99, 28, 56],
[76, 76, 75, 56, 49, 33, 51, 58, 41, 4],
[35, 55, 41, 7, 42, 85, 53, 14, 22, 51]])
np.mean(a, axis=1)
array([47.2, 57. , 60.5, 60.4, 51.9, 40.5])
np.array([np.mean(a[i,:]) for i in range(a.shape[0])])
array([47.2, 57. , 60.5, 60.4, 51.9, 40.5])
%timeit np.mean(a, axis=1)
10.8 µs ± 2.4 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each)
%timeit np.array([np.mean(a[i,:]) for i in range(a.shape[0])])
43.7 µs ± 925 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
Preguntate siempre si puedes vectorizar algo y hazlo. Por ejemplo, Para dos matrices (grandes).
a = np.random.randint(100, size=(1000,100))
b = np.random.randint(200, size=(1000,100))
# El número de elementos que son iguales
np.mean(a==b)
0.00512
# El promedio de los elementos de a que son mayores a su correspondiente posición en b
np.mean(a[a>b])
66.36604323536555
# El promedio de los elementos de b que son mayores a su correspondiente posición en a
np.mean(b[b>a])
122.37378653758725
# Con matrices más pequeñas
a = np.random.randint(100, size=(10))
b = np.random.randint(200, size=(10))
print (a)
print (b)
[73 19 71 47 95 38 48 59 74 61]
[ 68 94 69 142 167 40 190 70 33 95]
# el elemento en b correspondiente a la posición del elemento más grande en a
b[np.argmax(a)]
167
Broadcasting#
Normalmente, Numpy necesita que las dimensiones de las matrices coincidan cuando se hacen operaciones con ellas
a = np.random.randint(100, size=(3,5))
b = np.random.randint(10, size=(3,4))
print (a)
print (b)
a + b
[[83 58 25 73 33]
[91 73 70 60 18]
[20 86 0 23 62]]
[[7 2 4 0]
[3 6 7 1]
[7 9 5 2]]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-14-860cc8167430> in <cell line: 5>()
3 print (a)
4 print (b)
----> 5 a + b
ValueError: operands could not be broadcast together with shapes (3,5) (3,4)
Pero numoy intentan expandir las operaciones si alguna de las dimensiones coincide
a
array([[83, 58, 25, 73, 33],
[91, 73, 70, 60, 18],
[20, 86, 0, 23, 62]])
a*10
array([[830, 580, 250, 730, 330],
[910, 730, 700, 600, 180],
[200, 860, 0, 230, 620]])
# Veamos como funciona el reshape en la siguiente operación.
a + b[:,1].reshape(-1,1)
array([[85, 60, 27, 75, 35],
[97, 79, 76, 66, 24],
[29, 95, 9, 32, 71]])
b[:,1].reshape(-1,1)
array([[2],
[6],
[9]])
b[:,1]
array([2, 6, 9])
a + b[:,1]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-20-d148e74cc6fe> in <cell line: 1>()
----> 1 a + b[:,1]
ValueError: operands could not be broadcast together with shapes (3,5) (3,)
# Observa la forma de las filas
a + b.flatten()[:a.shape[1]]
array([[90, 60, 29, 73, 36],
[98, 75, 74, 60, 21],
[27, 88, 4, 23, 65]])
print (a)
print (b)
[[83 58 25 73 33]
[91 73 70 60 18]
[20 86 0 23 62]]
[[7 2 4 0]
[3 6 7 1]
[7 9 5 2]]
b.flatten()
array([7, 2, 4, 0, 3, 6, 7, 1, 7, 9, 5, 2])
b.flatten()[:a.shape[1]]
array([7, 2, 4, 0, 3])
Expresiones compactas / Comprehensions#
Fíjate cómo las siguientes expresiones son equivalentes:
a=15
if a > 10:
s = "mayor que 10"
else:
s = "menor que 10"
print(s)
mayor que 10
a = 15
s = "mayor que 10" if a > 10 else "menor que 10"
print(s)
mayor que 10
l=[]
for i in range(5):
l.append(i)
print(l)
[0, 1, 2, 3, 4]
l=[i for i in range(5)]
print(l)
[0, 1, 2, 3, 4]
a = [10, -4, 20, 5]
#o = ["10A", "-4B", "20A", "5A"]
o = []
for i in a:
if i<0:
o.append(str(i)+"B")
else:
o.append(str(i)+"A")
print(o)
['10A', '-4B', '20A', '5A']
a = [10, -4, 20, 5]
def convert(x):
return str(x)+"B" if x<0 else str(x)+"A"
o = [convert(i) for i in a]
print(o)
['10A', '-4B', '20A', '5A']
r = []
for i in range(10):
r.append("el numero "+str(i))
print(r)
['el numero 0', 'el numero 1', 'el numero 2', 'el numero 3', 'el numero 4', 'el numero 5', 'el numero 6', 'el numero 7', 'el numero 8', 'el numero 9']
r = ["el numero "+str(i) for i in range(10)]
print(r)
['el numero 0', 'el numero 1', 'el numero 2', 'el numero 3', 'el numero 4', 'el numero 5', 'el numero 6', 'el numero 7', 'el numero 8', 'el numero 9']
frutas = {'Fresa':'roja', 'Limon':'verde', 'Papaya':'naranja', 'Manzana':'amarilla', 'Guayaba':'rosa'}
for nombre, color in frutas.items():
print (nombre, "es de color", color)
print()
r = [nombre+" es de color "+color for nombre, color in frutas.items()]
r
Fresa es de color roja
Limon es de color verde
Papaya es de color naranja
Manzana es de color amarilla
Guayaba es de color rosa
['Fresa es de color roja',
'Limon es de color verde',
'Papaya es de color naranja',
'Manzana es de color amarilla',
'Guayaba es de color rosa']
Ejercicio#
Construir una matriz aleatoria de cuatro letras (A,T,C,G) de tamaño 100x1000 luego cambiar las letras por las siguientes codificaciones:
Codificación 1: -2,-1,1,2
Codificación 2: 0,1,2,3
Codifiación 3: 0001,0010,0100,1000
m=np.array([['A','T'],['C','G']])
m
array([['A', 'T'],
['C', 'G']], dtype='<U1')
Matplotlib#
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
x = np.linspace(-4,4,20)# El vector de tabulación
y=x**2
z=x**3
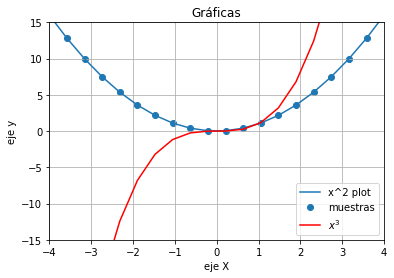
plt.plot(x, y, label="x^2 plot")
plt.scatter(x, y, label="muestras")
plt.plot(x, z, label="$x^3$", color="red")
plt.xlim([-4,4])
plt.ylim([-15, 15])
plt.legend()
plt.grid(True)
plt.xlabel('eje X')
plt.ylabel('eje y')
plt.title('Gráficas')
Text(0.5, 1.0, 'Gráficas')
x = np.linspace(-4,4,20)
y=x**2
plt.figure(figsize=(10,10))
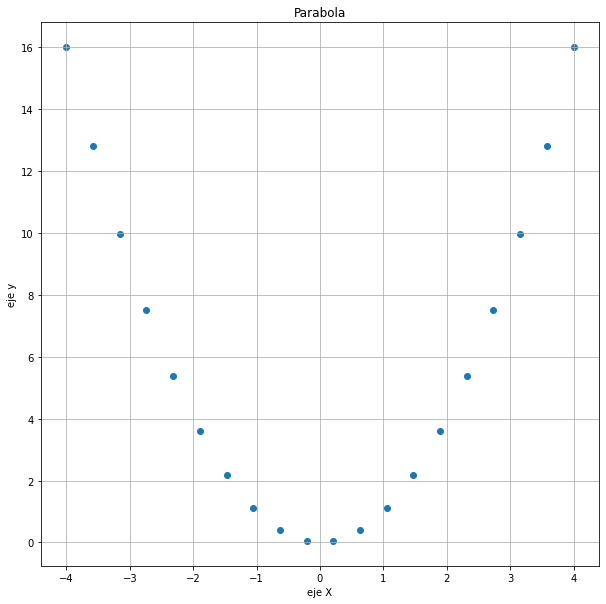
plt.scatter(x, y)
plt.grid(True)
plt.xlabel('eje X')
plt.ylabel('eje y')
plt.title('Parabola')
plt.figure(figsize=(10,10))
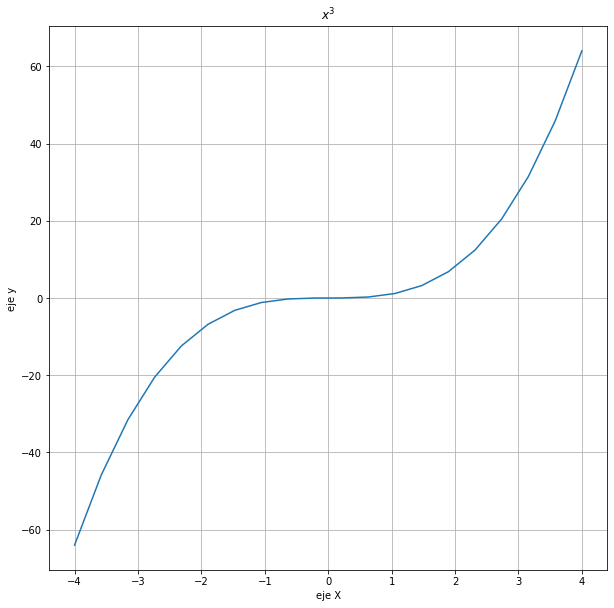
plt.plot(x, x**3)
plt.grid(True)
plt.xlabel('eje X')
plt.ylabel('eje y')
plt.title('$x^3$')
Text(0.5, 1.0, '$x^3$')
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.figure(figsize=(10,10))
x = np.linspace(-4,4,10)
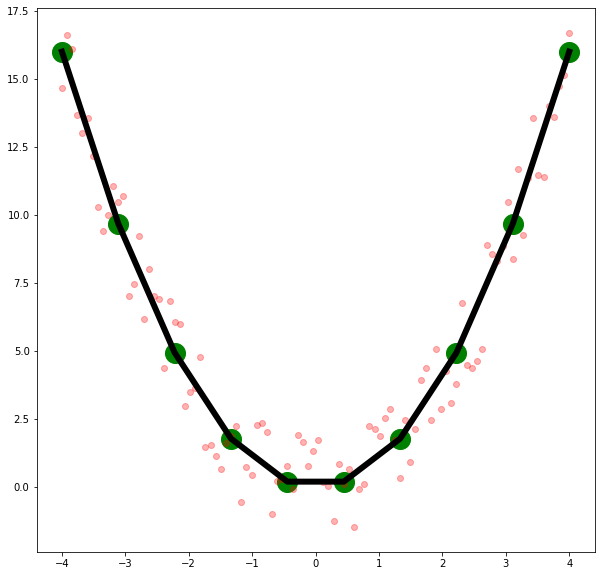
plt.plot(x, x**2, color="black", linewidth=6)
plt.scatter(x, x**2, c="green", s=400)
x_r = np.linspace(-4,4,100)
x_ruido = x_r**2 + (np.random.random(x_r.shape)-0.5)*4
plt.scatter(x_r,x_ruido, c="red", alpha=0.3)
<matplotlib.collections.PathCollection at 0x7ff4845f44f0>
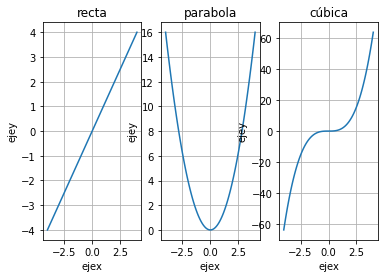
x=np.linspace(-4,4,100)
y=x
z=x**2
w=x**3
#plt.figure()
plt.subplot(1,3,1)
plt.plot(x,y)
plt.xlabel('ejex')
plt.ylabel('ejey')
plt.title('recta')
plt.grid()
#plt.figure()
plt.subplot(1,3,2)
plt.plot(x,z)
plt.xlabel('ejex')
plt.ylabel('ejey')
plt.title('parabola')
plt.grid()
#plt.figure()
plt.subplot(1,3,3)
plt.plot(x,w)
plt.xlabel('ejex')
plt.ylabel('ejey')
plt.title('cúbica')
plt.grid()
Imágenes#
from google.colab import drive
drive.mount('/content/drive')
Mounted at /content/drive
#Rei
#path_data = "/content/drive/MyDrive/Machine Learning 2023-1 UManizales Maestría/Clase 2/Data"
#Arteaga
path_data = "/content/drive/MyDrive/Clases 2023-01/Programación Concurrente y Distribuida/Semana 2-3/Introducción a Python/Data"
path_mesa = path_data+"/Mesa.jpg"
path_chestxray = path_data+"/ChestXRay.jpg"
from skimage import io
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
#Arteaga
img = io.imread(path_mesa)
img2 = io.imread(path_chestxray)
print("dimensiones", img.shape, "max", np.max(img), "min", np.min(img), "tipo",type(img))
plt.scatter(320,100, marker="x", s=200, linewidth=7, c="b")
plt.scatter(150,230, marker="x", s=200, linewidth=5, c="g")
print("pixel at blue marker ", img[100,320,:])
print("pixel at green marker", img[230,150,:])
img[100,:,:]=0
img[150,:,:]=255
#plt.grid() # remove gridlines
plt.imshow(img)
dimensiones (246, 360, 3) max 255 min 0 tipo <class 'numpy.ndarray'>
pixel at blue marker [75 0 5]
pixel at green marker [ 24 48 112]
<matplotlib.image.AxesImage at 0x7ff45c6ccf10>

img
array([[[ 90, 108, 132],
[224, 254, 254],
[ 64, 110, 143],
...,
[173, 188, 191],
[144, 162, 164],
[172, 189, 196]],
[[ 34, 61, 80],
[212, 223, 241],
[156, 201, 230],
...,
[173, 192, 198],
[173, 193, 200],
[158, 187, 191]],
[[ 27, 57, 83],
[134, 141, 157],
[172, 231, 247],
...,
[195, 205, 207],
[188, 193, 197],
[175, 186, 190]],
...,
[[ 44, 52, 55],
[ 36, 45, 52],
[ 38, 43, 46],
...,
[119, 113, 97],
[120, 122, 109],
[122, 125, 130]],
[[ 57, 47, 38],
[ 54, 46, 43],
[ 55, 52, 47],
...,
[109, 99, 87],
[113, 110, 91],
[105, 108, 101]],
[[ 58, 56, 57],
[ 69, 70, 65],
[ 61, 66, 69],
...,
[139, 133, 119],
[134, 119, 98],
[132, 123, 108]]], dtype=uint8)
img = io.imread(path_mesa)
img[:,:,1]=0
img[:,:,2]=0
plt.imshow(img)
img = io.imread(path_mesa)
img[:,:,0]=0
img[:,:,2]=0
plt.figure()
plt.imshow(img)
img = io.imread(path_mesa)
img[:,:,0]=0
img[:,:,1]=0
plt.figure()
plt.imshow(img)
<matplotlib.image.AxesImage at 0x7ff45c4e0310>



img = io.imread(path_mesa)
plt.imshow(img[:,:,1])
plt.figure()
plt.imshow(img[:,:,1], cmap = plt.cm.Greys_r)
<matplotlib.image.AxesImage at 0x7ff45c3c1700>


# Otra imagen
print(img2.shape)
plt.imshow(img2)
(718, 1418, 3)
<matplotlib.image.AxesImage at 0x7ff45c3cd940>
La manipulación de imágenes se reduce a realizar cálculos sobre los valores de luminosidad de cada pixel. Por ejemplo, obtenemos una versión en escala de grises promediando los valores RGB de cada pixel. Esto se hace de manera natural con la función np.mean y el argumento axis adecuado.
gimg = np.mean(img, axis=2)
print("dimensiones", gimg.shape, "max", np.max(gimg), "min", np.min(gimg))
plt.scatter(320,100, marker="x", s=200, linewidth=5, c="b")
plt.scatter(150,230, marker="x", s=200, linewidth=5, c="g")
print(img[100,320,:])
print("pixel at blue marker ", gimg[100,320])
print("pixel at green marker", gimg[230,150])
#plt.grid() # remove gridlines
plt.imshow(gimg, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
dimensiones (246, 360) max 255.0 min 0.0
[75 0 5]
pixel at blue marker 26.666666666666668
pixel at green marker 61.333333333333336
<matplotlib.image.AxesImage at 0x7ff45c182640>

Ejercicio#
También podemos acceder a porciones (parches) de la imagen usando la notación natural de matrices de Python. Si además, reducimos la luminosidad de cada pixel a la mitad lo que hacemos es oscurecer la imagen.
Cargar nuevamente la imagen de la mesa
Visualizarla
Obtener una nueva imágen promediando los 3 canales RGB
Visualizarla
Extraer el jarron de la posición 50:100 y 300:350 (ver imagen anterior)
Visualizarla
Dividir todos los pixeles del parche extraido (item 5) entre 2
Compara los parches (visualiza usando los parámetros: cmap=”gray”, vmin=0, vmax=255), el original y el de división de cada pixel entre 2 ¿Qué observa?
# Escribe tu código aquí
gimg = np.mean(img, axis=2)
plt.imshow(gimg, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
<matplotlib.image.AxesImage at 0x7ff45c160760>

gimg2=gimg/2
plt.imshow(gimg2, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
<matplotlib.image.AxesImage at 0x7ff45c0a1b80>

jarron=gimg[50:100 , 300:350 ]
plt.imshow(jarron, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
<matplotlib.image.AxesImage at 0x7ff44ecbee80>

jarronOscurito=jarron/2
plt.imshow(jarronOscurito, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
<matplotlib.image.AxesImage at 0x7ff44ec2b160>

plt.subplot(1,2,1)
plt.imshow(jarron, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
plt.subplot(1,2,2)
plt.imshow(jarronOscurito, cmap = plt.cm.Greys_r, vmin=0, vmax=255)
<matplotlib.image.AxesImage at 0x7ff44e835fa0>

