Numpy#
Con la librería numpy se trabaja con matrices de forma natural. Fíjate cómo se declaran y cómo descubrimos sus dimensiones.
https://s3.amazonaws.com/assets.datacamp.com/blog_assets/Numpy_Python_Cheat_Sheet.pdf
import numpy as np
a = np.array([[1,2,3,4,5],
[5,4,3,2,1],
[9,8,7,6,5],
[7,6,5,6,7],
[2,2,2,3,3],
[4,3,4,3,4],
[5,1,1,4,1]]).astype('int32')
print(a, type(a),a.nbytes,"\n")
print("a shape", a.shape,"\n")
print("a rows", a.shape[0],"\n")
print("a cols", a.shape[1])
[[1 2 3 4 5]
[5 4 3 2 1]
[9 8 7 6 5]
[7 6 5 6 7]
[2 2 2 3 3]
[4 3 4 3 4]
[5 1 1 4 1]] <class 'numpy.ndarray'> 140
a shape (7, 5)
a rows 7
a cols 5
a[0,0]=100
a
array([[100, 2, 3, 4, 5],
[ 5, 4, 3, 2, 1],
[ 9, 8, 7, 6, 5],
[ 7, 6, 5, 6, 7],
[ 2, 2, 2, 3, 3],
[ 4, 3, 4, 3, 4],
[ 5, 1, 1, 4, 1]], dtype=int32)
a.nbytes
140
v = np.array([2,3,4,5,6,7,3,12])
print("v shape", v.shape)
print("v elems", v.shape[0])
print(v, type(v))
v shape (8,)
v elems 8
[ 2 3 4 5 6 7 3 12] <class 'numpy.ndarray'>
v[3:-1]
array([5, 6, 7, 3])
np.min(v), np.max(v)
(2, 12)
Con la notación de índices accedemos a columas o filas enteras, rangos de columnas o filas, elementos individuales o porciones de una matriz o un vector.
print("una fila " ,a[2])
print("una fila " ,a[2,:])
print("una columna " ,a[:,2])
print("un elemento " ,a[2,2])
print("varias filas \n",a[2:5])
print("varias columnas \n",a[:,1:3])
print("una porcion \n",a[2:5,1:3])
una fila [9 8 7 6 5]
una fila [9 8 7 6 5]
una columna [3 3 7 5 2 4 1]
un elemento 7
varias filas
[[9 8 7 6 5]
[7 6 5 6 7]
[2 2 2 3 3]]
varias columnas
[[2 3]
[4 3]
[8 7]
[6 5]
[2 2]
[3 4]
[1 1]]
una porcion
[[8 7]
[6 5]
[2 2]]
Muchas funciones de la librería numpy operan sobre una matriz completa, o de forma separada por columnas o filas según el valor del argumento axis.
print(a)
print("suma total", np.sum(a))
print("suma eje 0", np.sum(a, axis=0))
print("suma eje 1", np.sum(a, axis=1))
print("promedio total", np.mean(a))
print("promedio eje 0", np.mean(a, axis=0))
print("promedio eje 1", np.mean(a, axis=1))
[[100 2 3 4 5]
[ 5 4 3 2 1]
[ 9 8 7 6 5]
[ 7 6 5 6 7]
[ 2 2 2 3 3]
[ 4 3 4 3 4]
[ 5 1 1 4 1]]
suma total 237
suma eje 0 [132 26 25 28 26]
suma eje 1 [114 15 35 31 12 18 12]
promedio total 6.771428571428571
promedio eje 0 [18.85714286 3.71428571 3.57142857 4. 3.71428571]
promedio eje 1 [22.8 3. 7. 6.2 2.4 3.6 2.4]
Las matrices en Python pueden tener un número arbitrario de dimensiones y podemos acceder a submatrices en la dirección o dimensión que queramos.
z = np.random.randint(-20,20, size=(5,5))
print(z)
[[-19 4 -13 -19 13]
[ 19 6 -9 -9 -16]
[-11 12 -6 -20 16]
[ -4 -1 -4 13 0]
[-19 13 -1 9 8]]
np.sum(z, axis=1)
array([-34, -9, -9, 4, 10])
#m = np.random.randint(10, size=(3,3,3))
print("Matrix 3D completa\n", m)
print("----------\n", m[0,:,:])
print("----------\n", m[1,:,:])
print("----------\n", m[:,0,:])
print("----------\n", m[:,0,1])
print("----------\n", np.mean(m, axis=1))
Matrix 3D completa
[[[7 0 8]
[4 0 4]
[3 4 9]]
[[4 7 9]
[2 2 6]
[0 5 9]]
[[8 6 9]
[0 3 0]
[0 9 2]]]
----------
[[7 0 8]
[4 0 4]
[3 4 9]]
----------
[[4 7 9]
[2 2 6]
[0 5 9]]
----------
[[7 0 8]
[4 7 9]
[8 6 9]]
----------
[0 7 6]
----------
[[4.66666667 1.33333333 7. ]
[2. 4.66666667 8. ]
[2.66666667 6. 3.66666667]]
m.shape
(3, 3, 3)
m
Generación de matrices y vectores#
print("matrix identidad\n", np.eye(3))
print("vector de ceros", np.zeros(4))
print("matriz de ceros\n", np.zeros((3,2)))
print("matriz de unos\n", np.ones((2,3)))
print("vector rango", np.arange(10))
print("vector rango", np.arange(5,10))
print("vector espacio lineal", np.linspace(2,12,11))
print("matriz aleatoria según distribución uniforme [0,1]\n", np.random.random(size=(3,5)))
print("vector aleatorio de enteros entre 0 y 5", np.random.randint(5, size=10))
matrix identidad
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
vector de ceros [0. 0. 0. 0.]
matriz de ceros
[[0. 0.]
[0. 0.]
[0. 0.]]
matriz de unos
[[1. 1. 1.]
[1. 1. 1.]]
vector rango [0 1 2 3 4 5 6 7 8 9]
vector rango [5 6 7 8 9]
vector espacio lineal [ 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.]
matriz aleatoria según distribución uniforme [0,1]
[[0.57996022 0.65361661 0.99420518 0.12111156 0.26731741]
[0.206147 0.25575192 0.66588831 0.55022348 0.76820253]
[0.51384056 0.63172996 0.50836505 0.41256526 0.66835632]]
vector aleatorio de enteros entre 0 y 5 [0 3 3 0 3 3 2 1 2 1]
Operaciones vectorizadas#
import numpy as np
v = np.array([10,12,13,15,20])
print(v)
print(v+1)
print(v*2)
a = np.random.randint(100, size=5)
print(a)
print(v.dot(a))
[10 12 13 15 20]
[11 13 14 16 21]
[20 24 26 30 40]
[60 83 36 31 82]
4169
Las operaciones vectorizadas también funcionan con expresiones booleanas. Fíjate cómo se indexa un vector con una expresión booleana para seleccionar un conjunto de elementos.
a = np.array([1,8,4,10,-4,5])
print("posiciones en a >4:", a>4)
print("elementos de a >4:",a[a>4])
posiciones en a >4: [False True False True False True]
elementos de a >4: [ 8 10 5]
Expresiones compactas / Comprehensions#
Fíjate cómo las siguientes expresiones son equivalentes:
a=15
if a > 10:
s = "mayor que 10"
else:
s = "menor que 10"
print(s)
mayor que 10
a = 15
s = "mayor que 10" if a > 10 else "menor que 10"
print(s)
mayor que 10
l=[]
for i in range(5):
l.append(i)
print(l)
[0, 1, 2, 3, 4]
l=[i for i in range(5)]
print(l)
[0, 1, 2, 3, 4]
a = [10, -4, 20, 5]
#o = ["10A", "-4B", "20A", "5A"]
o = []
for i in a:
if i<0:
o.append(str(i)+"B")
else:
o.append(str(i)+"A")
print(o)
['10A', '-4B', '20A', '5A']
a = [10, -4, 20, 5]
def convert(x):
return str(x)+"B" if x<0 else str(x)+"A"
o = [convert(i) for i in a]
print(o)
['10A', '-4B', '20A', '5A']
r = []
for i in range(10):
r.append("el numero "+str(i))
print(r)
['el numero 0', 'el numero 1', 'el numero 2', 'el numero 3', 'el numero 4', 'el numero 5', 'el numero 6', 'el numero 7', 'el numero 8', 'el numero 9']
r = ["el numero "+str(i) for i in range(10)]
print(r)
['el numero 0', 'el numero 1', 'el numero 2', 'el numero 3', 'el numero 4', 'el numero 5', 'el numero 6', 'el numero 7', 'el numero 8', 'el numero 9']
frutas = {'Fresa':'roja', 'Limon':'verde', 'Papaya':'naranja', 'Manzana':'amarilla', 'Guayaba':'rosa'}
for nombre, color in frutas.items():
print (nombre, "es de color", color)
print()
r = [nombre+" es de color "+color for nombre, color in frutas.items()]
r
Fresa es de color roja
Limon es de color verde
Papaya es de color naranja
Manzana es de color amarilla
Guayaba es de color rosa
['Fresa es de color roja',
'Limon es de color verde',
'Papaya es de color naranja',
'Manzana es de color amarilla',
'Guayaba es de color rosa']
Ejercicio#
Construir una matriz aleatoria de cuatro letras (A,T,C,G) de tamaño 100x1000 luego cambiar las letras por las siguientes codificaciones:
Codificación 1: -2,-1,1,2
Codificación 2: 0,1,2,3
Codifiación 3: 0001,0010,0100,1000
m=np.array([['A','T'],['C','G']])
m
array([['A', 'T'],
['C', 'G']], dtype='<U1')
Matplotlib#
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
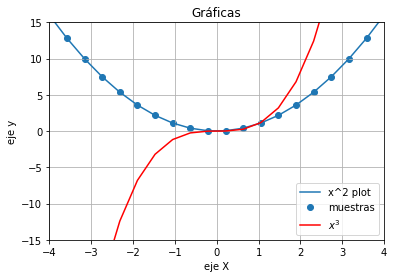
x = np.linspace(-4,4,20)# El vector de tabulación
y=x**2
z=x**3
plt.plot(x, y, label="x^2 plot")
plt.scatter(x, y, label="muestras")
plt.plot(x, z, label="$x^3$", color="red")
plt.xlim([-4,4])
plt.ylim([-15, 15])
plt.legend()
plt.grid(True)
plt.xlabel('eje X')
plt.ylabel('eje y')
plt.title('Gráficas')
Text(0.5, 1.0, 'Gráficas')
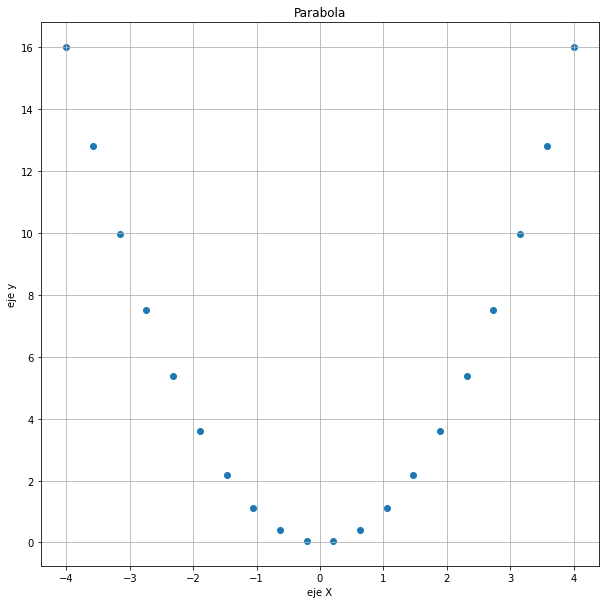
x = np.linspace(-4,4,20)
y=x**2
plt.figure(figsize=(10,10))
plt.scatter(x, y)
plt.grid(True)
plt.xlabel('eje X')
plt.ylabel('eje y')
plt.title('Parabola')
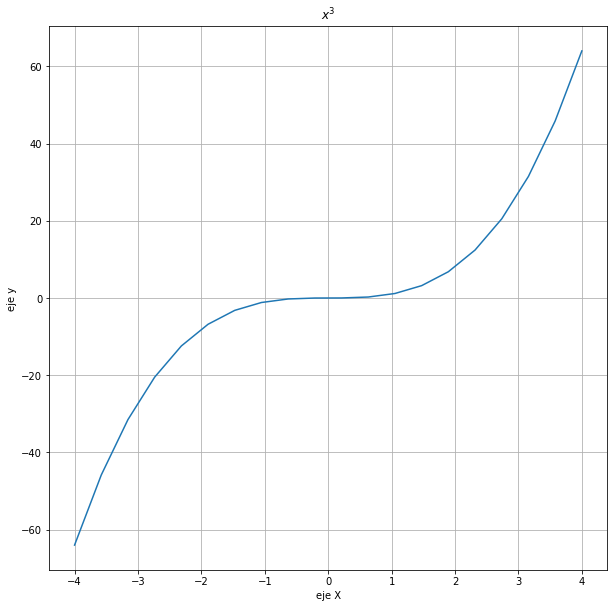
plt.figure(figsize=(10,10))
plt.plot(x, x**3)
plt.grid(True)
plt.xlabel('eje X')
plt.ylabel('eje y')
plt.title('$x^3$')
Text(0.5, 1.0, '$x^3$')
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
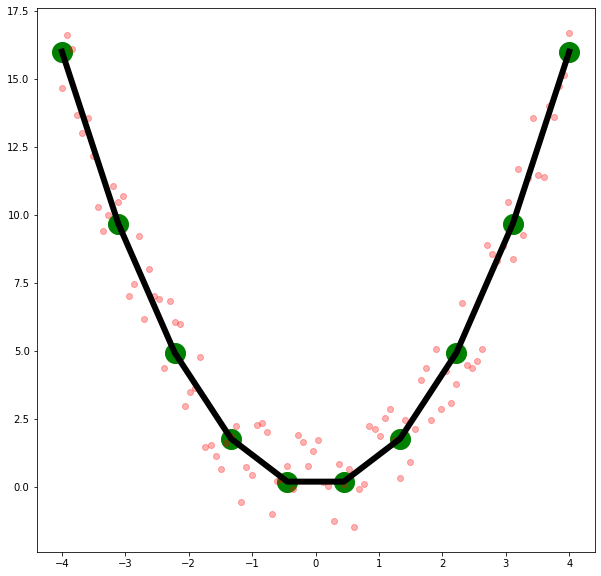
plt.figure(figsize=(10,10))
x = np.linspace(-4,4,10)
plt.plot(x, x**2, color="black", linewidth=6)
plt.scatter(x, x**2, c="green", s=400)
x_r = np.linspace(-4,4,100)
x_ruido = x_r**2 + (np.random.random(x_r.shape)-0.5)*4
plt.scatter(x_r,x_ruido, c="red", alpha=0.3)
<matplotlib.collections.PathCollection at 0x7ff4845f44f0>
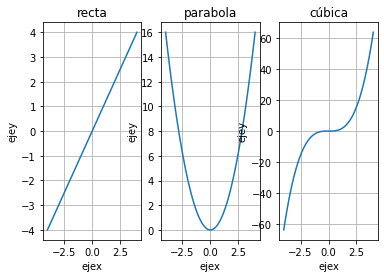
x=np.linspace(-4,4,100)
y=x
z=x**2
w=x**3
#plt.figure()
plt.subplot(1,3,1)
plt.plot(x,y)
plt.xlabel('ejex')
plt.ylabel('ejey')
plt.title('recta')
plt.grid()
#plt.figure()
plt.subplot(1,3,2)
plt.plot(x,z)
plt.xlabel('ejex')
plt.ylabel('ejey')
plt.title('parabola')
plt.grid()
#plt.figure()
plt.subplot(1,3,3)
plt.plot(x,w)
plt.xlabel('ejex')
plt.ylabel('ejey')
plt.title('cúbica')
plt.grid()