Unidad 3: Métricas de desempeño#
Contenido de la unidad#
Tiempo, aceleración, eficiencia y escalabilidad#
¿Cómo evaluar el desempeño de un programa paralelo?
Tiempo de ejecución#
Es el índice más básico. Se define como el intervalo de tiempo que transcurre desde el comienzo de la ejecución de la aplicación en el sistema paralelo hasta que el último proceso termina su ejecución.

Esta métrica es absoluta y permite medir el programa paralelo sin necesidad de compararlo con otro.
Aceleración#
La fórmula del Speed-Up se define como:
Donde:
\(T \cdot n\) representa el mejor tiempo de ejecución en modo secuencial.
\(T_p(N)\) representa el tiempo de ejecución en modo paralelo.
Aceleración
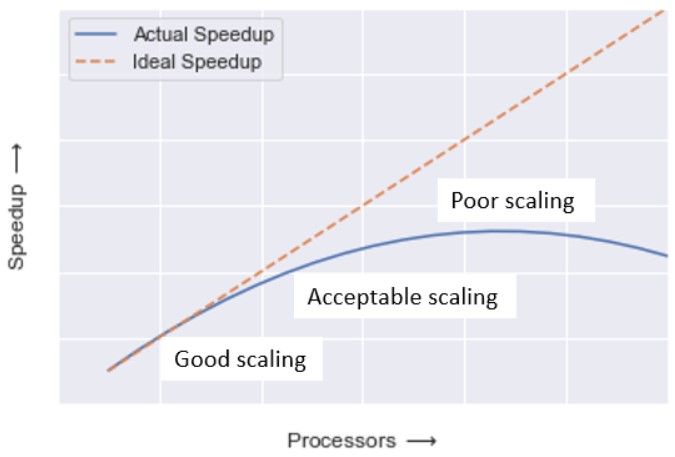
La aceleración varía de una máquina paralela a otra y en función de cómo se realice la paralelización.
Un mayor speedup es igual a más ganancia con la paralelización.
Eficiencia#
La eficiencia se calcula utilizando la siguiente fórmula:
Donde:
\(Eficiencia(p)\) es la eficiencia con \(p\) procesos. Con un valor entre 0 y 1. Su rendimiento puede verse afectado por el overhead.
\(Speed\_up(p)\) es el speed-up con \(p\) procesos.
\(p\) es la cantidad de procesos con los que se ejecuta la aplicación.
Eficiencia
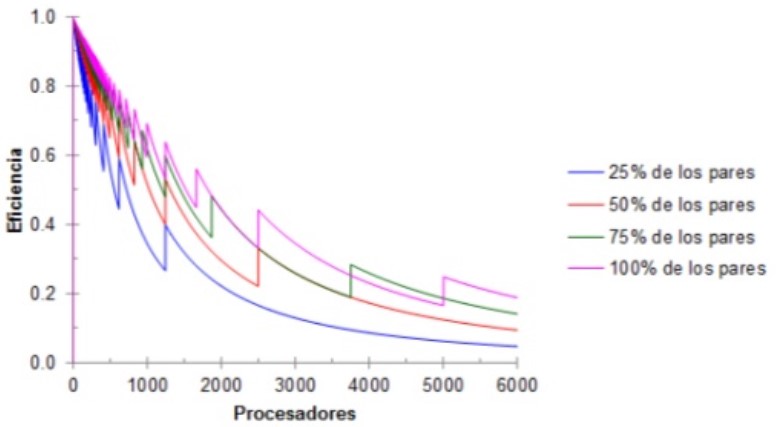
Paralelización y Eficiencia:
Idealmente, se espera una eficiencia de 1 en la paralelización, lo que significa que se ha logrado una paralelización total.
En la práctica, no todo el programa puede ser paralelizado.
Overhead:
El overhead se refiere al costo adicional asociado con la administración de la comunicación y sincronización entre procesos en la programación paralela.
Puede limitar la escalabilidad de un algoritmo y afectar el rendimiento.
El overhead incluye factores como el tiempo de inicio y terminación de tareas, sincronización, comunicación de datos y sobrecarga de software (lenguajes paralelos, bibliotecas, sistema operativo, etc.).
Es importante minimizar el overhead siempre que sea posible para lograr un alto rendimiento y una buena escalabilidad.
Escalabilidad#
Capacidad de un algoritmo de mantener sus prestaciones cuando aumenta el número de procesos y/o el tamaño del problema (workload).
Escalabilidad
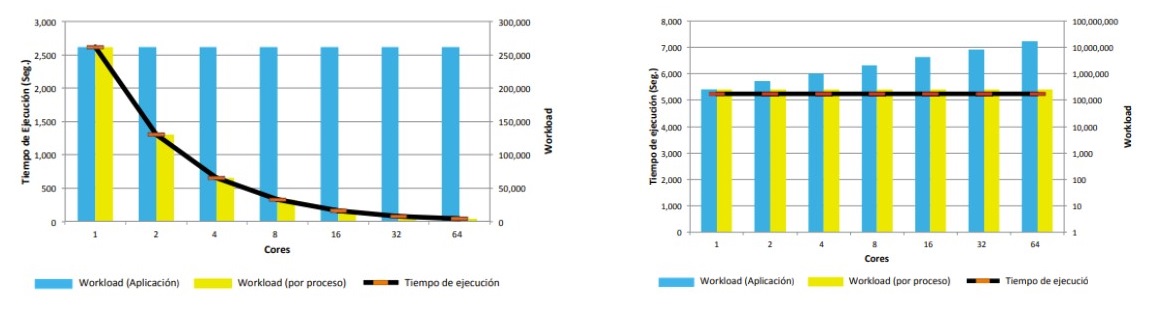
Esta característica nos permite evaluar el comportamiento del sistema cuando se incrementa el número de procesos y/o el tamaño del proceso (workload)
Suele indicar la capacidad de una aplicación paralela para utilizar de forma eficiente un incremento en los recursos computacionales.
Una aplicación escalable suele ser capaz de mantener su eficiencia constante cuando aumentamos el número de procesos incluso a base de aumentar el tamaño del problema (datos de entrada).
Si un algoritmo no es escalable, aunque se aumente el número de procesos, no se conseguirá incrementar la eficiencia, con lo cual no se saca provecho de los cores del sistema
Escalabilidad Fuerte
El workload es constante. El objetivo es disminuir el tiempo de ejecución de la aplicación aumentando el número de procesos.
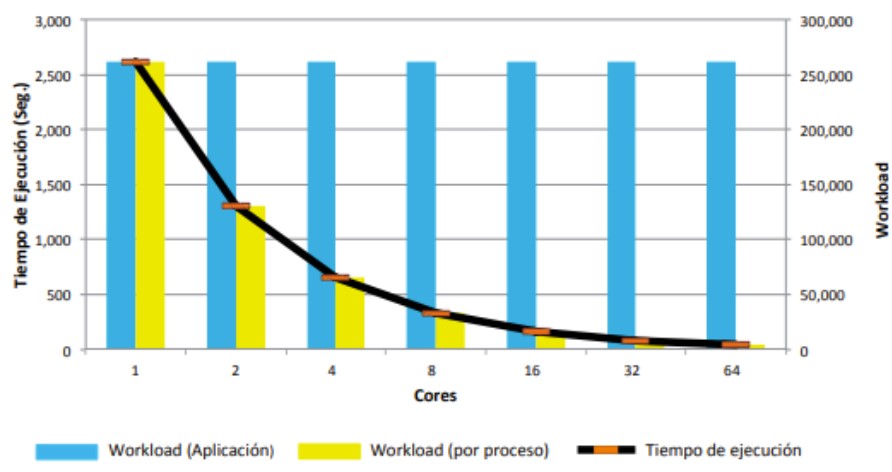
Está fuertemente relacionada con la ley de Amdahl (se verá a continuación).
Escalabilidad Débil
Se aumenta el número de procesos de la aplicación manteniendo el tamaño del problema para cada proceso constante, consiguiendo que el tiempo sea constante.
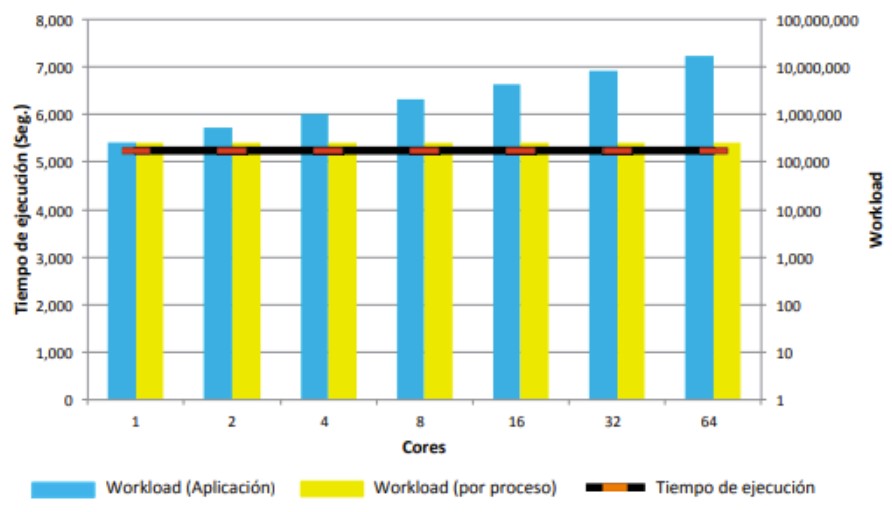
Se desprende de las observaciones de la ley de Gustafson (se verá a continuación).
Ley de Amdahl y Ley de Gustafson#
Ley de Amdahl#
Evalúa la máxima eficiencia que un algoritmo paralelo puede lograr con respecto a su versión serie. La ecuación \(S_p(n)\) se define de la siguiente manera:
Donde:
\(S_p(n)\) es la eficiencia de ejecución con \(n\) procesadores.
\(f\) es la fracción de código no paralelizable (en decimales).
\(p\) es el número de procesadores.
Ley de Amdahl
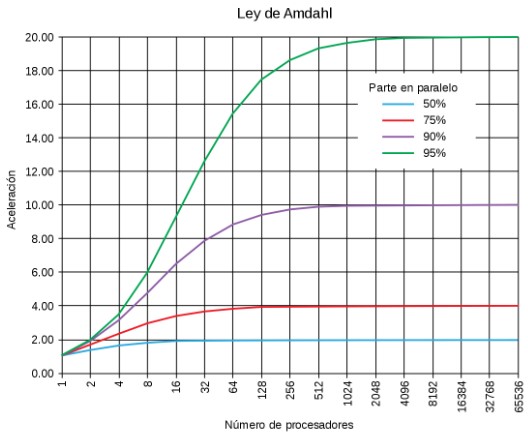
Eficiencia y Proporción Paralelizable:
La eficiencia está ligada a la proporción paralelizable de un algoritmo.
No depende de la cantidad de procesos utilizados en el cálculo.
Ley de Amdahl:
Formulada por Gene Amdahl, esta ley establece que la mejora en el rendimiento de un sistema está limitada por el tiempo que se utiliza un componente específico.
Identificar y reducir la fracción de código no paralelizable es crucial para mejorar el rendimiento de sistemas paralelos.
Identificación de Cuellos de Botella:
El aumento del rendimiento en sistemas se relaciona con la identificación de los cuellos de botella.
Mejorar la fracción de código no paralelizable es clave para aumentar la eficiencia.
Valor de la Mejora:
La Ley de Amdahl ayuda a determinar si una mejora en el sistema es significativa o no.
Simplificación y Limitaciones:
Es un modelo simplificado de la realidad y no considera factores como el overhead de comunicación y sincronización.
A pesar de sus limitaciones, sigue siendo una herramienta valiosa para comprender el rendimiento y la escalabilidad.
Nota
Importante revisar el Ejercicio de esta sección
Ley de Gustafson#
Establece que cualquier problema suficientemente grande puede ser eficientemente paralelizado, ofrece un nuevo punto de vista y así una visión positiva de las ventajas del procesamiento paralelo. La ecuación \(s\) se define de la siguiente manera:
Donde:
\(f\) es el porcentaje en decimales de la parte secuencial.
\(N\) es la cantidad de procesadores.
Ley de Gustafson
Gustafson consideraba que la ley de amdahl daba un límite para el descenso del tiempo de ejecución del algoritmo paralelo, dependiendo la fracción serie del algoritmo.
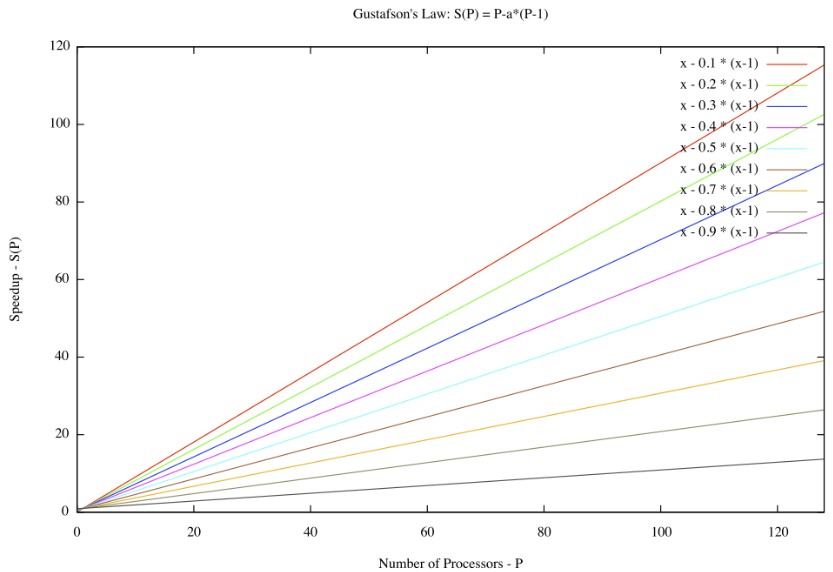
Sugiere que el tamaño del problema (N) aumenta a medida que se agregan más recursos, lo que significa que la fracción del código que no se puede paralelizar se vuelve menos importante. Por lo tanto, si se puede paralelizar una gran parte del código, la aceleración obtenida aumentará en consecuencia.
Ley de Moore y Ley de Huang#
Ley de Moore#
La Ley de Moore, formulada por Gordon Moore en 1965 como una predicción empírica inicialmente válida por 10 años, sigue siendo una tendencia notable en la tecnología.
Ley de Moore
Aunque no es una ley universal, ha sido utilizada para describir el crecimiento exponencial de la capacidad de procesamiento y almacenamiento en dispositivos electrónicos.
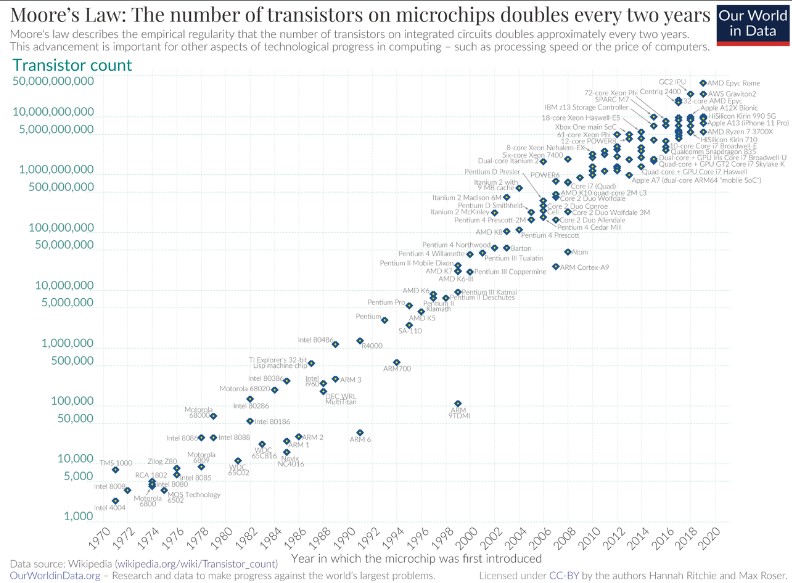
La idea central es que al aumentar la cantidad de transistores en un chip, se logra un incremento en la potencia y eficiencia de los dispositivos. Aunque inicialmente predijo un duplicado anual de transistores, en realidad se cumplió aproximadamente cada dos años.
Ley de Huang#
Sugiere que la velocidad de procesamiento puede aumentar proporcionalmente con el número de procesadores, pero solo hasta cierto punto.
No busca sustituir a la ley de Moore.
Cambio de paradigma en la computación. Buscan algoritmos que se sustenten en la paralelización de los datos. (La naturaleza del DL)
Ley de Huang

Es importante tener en cuenta la eficiencia límite al diseñar sistemas paralelos para garantizar que se utilicen los recursos adecuados y se logre el máximo rendimiento posible.
Precisión Simple Vs Precisión Doble y TFlops#
Enlaces de interés:
Truco
Diferencia entre precisión simple y precisión doble – Barcelona Geeks
Introducción a la Representación de Punto Flotante – Part 1 – Barcelona Geeks
A continuación encuentras una tabla comparando la precisión simple contra la precisión doble.
| PRECISIÓN SIMPLE | PRECISIÓN DOBLE |
|---|---|
| En precisión simple, se utilizan 32 bits para representar el número de coma flotante. | En doble precisión, se utilizan 64 bits para representar números de coma flotante. |
| Utiliza 8 bits para el exponente. | Utiliza 11 bits para exponente. |
| En precisión simple, se utilizan 23 bits para mantisa. | En doble precisión, se utilizan 52 bits para mantisa. |
| El número de sesgo es 127. | El número de sesgo es 1023. |
| Rango de números en precisión simple: 2-126 a 2+127. | Rango de números en doble precisión: 2-1022 a 2+1023. |
| Esto se usa cuando la precisión importa menos. | Esto se usa cuando la precisión es más importante. |
| Se utiliza para una amplia representación. | Se utiliza para la minimización de la aproximación. |
| Se utiliza en programas simples como juegos. | Se utiliza en programas complejos como calculadora científica. |
| Esto se llama binary32. | Esto se llama binary64. |
Conversión de números en punto flotante a binario: Precisión simple#
Algoritmo para convertir un número flotante a binario:
Se establece el bit del signo: negativo(1); positivo (0)
Convertir la parte entera a binario.
Convertir la parte fraccionaria (mantissa) de 23 bits
Escribir el número en notación científica
Reescribir el estándar IEEE754 32 bits

Vamos a convertir -3.6245 a binario en precisión simple:
1. El signo negativo se representa con un bit \(1_{(2)}\).

2. La parte entera es 3, que se representa \(11_{(2)}\) que se representa con 2 bits.
3. Convertimos parte fraccionaria: 0.6245 a binario
0.6245 x 2 = 1.2490 -> 1
0.2490 x 2 = 0.4980 -> 0
0.4980 x 2 = 0.9960 -> 0
0.9960 x 2 = 1.9920 -> 1
0.9920 x 2 = 1.9840 -> 1
0.9840 x 2 = 1.9680 -> 1
0.9680 x 2 = 1.9360 -> 1
0.9360 x 2 = 1.8720 -> 1
0.8720 x 2 = 1.7440 -> 1
0.7440 x 2 = 1.4880 -> 1 … Hasta tener 23 bits
R/ 1 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 \(_{(2)}\)
4. Convertimos el número a notación científica

5. Tomamos el exponente y le sumamos 127 del exceso
127 +1 = 128 = 10000000\(_{(2)}\)

Conversión de números en punto flotante a binario: Precisión doble#
Un nuevo ejercicio
Calcular la representación en precisión doble del mismo número (-3.6245) …

La entrega debe anexarse al final de la entrega del Ejercicio de esta sección.
Cálculo de Teraflops (TFlops)#
Los FLOPS (Floating Point Operations Per Second) son una medida del rendimiento de una computadora, y te permiten evaluar la capacidad de procesamiento de operaciones de punto flotante. Para calcular los FLOPS teóricos de una computadora portátil, generalmente puedes seguir los siguientes pasos, dependiendo de los componentes principales de la misma, especialmente la CPU y la GPU:
FLOPS en unidades

1. Identificar la arquitectura de la CPU/GPU#
Cada procesador tiene una arquitectura específica (por ejemplo, x86, ARM, etc.), lo que afecta la cantidad de operaciones que puede realizar en un ciclo de reloj.
2. Conseguir el número de núcleos y la frecuencia del reloj (GHz)#
Debes conocer cuántos núcleos físicos y lógicos tiene el procesador, así como su frecuencia de reloj. Puedes obtener esta información con programas como CPU-Z o con herramientas integradas en el sistema operativo (por ejemplo, en Windows mediante el «Administrador de tareas»).
3. Determinar el número de operaciones por ciclo#
Para esto, necesitas saber cuántas operaciones de punto flotante puede realizar el procesador por ciclo de reloj en cada núcleo. Esto dependerá de la arquitectura del procesador y si soporta instrucciones vectoriales avanzadas como AVX o AVX-512.
4. Calcular los teraflops#
Donde:
\(\text{Frecuencia de reloj de la CPU}\): es la Frecuencia de reloj de la CPU en hertz (Hz).
\(\text{Número de núcleos de la CPU}\): es la cantidad de núcleos de procesamiento de la CPU.
\(\text{Cantidad de operaciones por ciclo de reloj}\): es la cantidad de operaciones de punto flotante que se pueden realizar en cada ciclo de reloj.
\(10^{12}\): es un factor de escala para convertir los resultados a teraflops.
Nota
Ejemplo 1
Si una máquina tiene una velocidad de reloj de 3.5 GHz, 16 núcleos de procesamiento, 2 operaciones de punto flotante por ciclo de reloj y utiliza precisión doble, el cálculo de los teraflops sería?
Solución Ejemplo 1
TFLOPS = (3.5x10^9 x 16 x 2 ) / 10^12 = 0.112 TFLOPS
Nota
Ejemplo 2
Tres dispositivos tienen la misma frecuencia de reloj (2 GHz) y 4 núcleos de procesamiento cada uno. ¿Será que los dispositivos son igual de potentes?. Acá hay algunos datos para poder determinarlo…

Solución Ejemplo 2
Celular [2 GHz * 4 núcleos * (4*2 operaciones por ciclo)]/ (10^12) = 0.064 TFlops
Xbox [2 GHz * 4 núcleos * 6 operaciones por ciclo]/ (10^12) = 0.048 TFlops
Computador [2 GHz * 4 núcleos * (8*2 operaciones por ciclo)]/ (10^12) = 0.128 Tflops
Cálculo de Teraflops en mi PC#
Vamos a calcular teóricamente los teraflops de una computadora portatil, usemos como ejemplo la siguiente computadora:
Computador portátil MSI GS65 Stealth Thin 8RF
Para calcular los FLOPS de la MSI GS65 Stealth Thin 8RF, necesitamos considerar tanto la CPU como la GPU.
CPU (Intel Core i7-8750H)#
La laptop utiliza un procesador Intel Core i7-8750H que tiene 6 núcleos y 12 hilos, con una frecuencia base de 2.2 GHz y un turbo de hasta 4.1 GHz. Este procesador es capaz de realizar varias operaciones de punto flotante por ciclo, gracias a tecnologías como AVX.
Usaremos la frecuencia turbo de 4.1 GHz para el cálculo:
Núcleos: 6
Frecuencia: 4.1 GHz (4.1 x 10⁹ Hz)
Operaciones por ciclo (AVX2): Suponemos 16 operaciones de punto flotante por ciclo por núcleo, basándonos en las instrucciones AVX2.
Cálculo:
FLOPS_CPU = 6 núcleos × 4.1 × 10^9 Hz × 16 operaciones por ciclo = 393.6 GFLOPS
GPU (NVIDIA GTX 1070 Max-Q)#
Para calcular los FLOPS (Floating Point Operations Per Second) de una GPU, puedes seguir una fórmula similar a la que se utiliza para calcular los FLOPS en una CPU, pero con algunos ajustes específicos para las GPUs, ya que suelen tener múltiples núcleos (shaders o CUDA cores en el caso de NVIDIA, o Stream Processors en AMD) y pueden ejecutar varias operaciones de punto flotante simultáneamente.
FLOPS = Número de núcleos × Frecuencia del núcleo (en GHz) × Operaciones por ciclo
Donde:#
Número de núcleos: Es el número de núcleos de procesamiento en la GPU. Estos son los llamados CUDA cores (NVIDIA) o Stream Processors (AMD).
Frecuencia del núcleo: La velocidad del reloj a la que operan los núcleos de la GPU. Esta se suele medir en GHz (1 GHz = 10⁹ ciclos por segundo).
Operaciones por ciclo: Cuántas operaciones de punto flotante puede realizar un núcleo en un ciclo de reloj. Esto depende del tipo de operaciones que realiza la GPU y si son de 32 bits (FP32) o de 64 bits (FP64). La mayoría de las GPUs realizan dos operaciones de coma flotante por ciclo en FP32.
Cálculo paso a paso:#
1. Número de núcleos:#
Por ejemplo, una GPU NVIDIA GTX 1070 tiene 2,048 CUDA cores.
2. Frecuencia del núcleo:#
Supongamos que la GPU tiene una frecuencia de 1.215 GHz.
3. Operaciones por ciclo:#
En el caso de operaciones de punto flotante de 32 bits (FP32), cada núcleo puede realizar dos operaciones de punto flotante por ciclo.
Ejemplo de cálculo para FP32:#
FLOPS (FP32) = 2,048 núcleos × 1.215 GHz × 2 operaciones por ciclo
= 2,048 × 1.215 × 2
= 4,976.64 GFLOPS
= 4.976 TFLOPS
Total FLOPS estimados (CPU + GPU):#
CPU: 393.6 GFLOPS
GPU: 4976.64 GFLOPS
Total: Aproximadamente 5370.24 GFLOPS (5.370 TFLOPS).
Este cálculo da una estimación teórica del rendimiento de la laptop en operaciones de punto flotante, tomando en cuenta tanto la CPU como la GPU.
¿Realmente está bien calculado?#
Los cálculos de FLOPS generalmente se refieren a la cantidad de operaciones de punto flotante por segundo en una arquitectura de 32 bits (FP32) o 64 bits (FP64), dependiendo del tipo de cálculo que se esté realizando.
FLOPS de CPU: • En el caso de la Intel Core i7-8750H, las operaciones de punto flotante suelen realizarse en 64 bits (FP64) cuando se utilizan instrucciones estándar. Sin embargo, si la CPU usa instrucciones vectoriales como AVX o AVX2, estas pueden operar con datos de 32 bits (FP32), lo que duplica la cantidad de operaciones de punto flotante por ciclo.
FLOPS de GPU: • La GTX 1070 Max-Q está optimizada para operaciones de 32 bits (FP32), que es el estándar en las GPUs para cálculos en gráficos y muchos cálculos científicos. Aunque las GPUs también pueden realizar operaciones de 64 bits (FP64), su rendimiento es significativamente menor en comparación con las operaciones FP32.
En Conclusión:
• Los cálculos que hicimos se basan en operaciones de 32 bits (FP32), ya que tanto la GPU como las instrucciones AVX de la CPU tienden a realizar más operaciones de este tipo. Si estuviéramos calculando FLOPS para operaciones de 64 bits (FP64), el rendimiento sería menor, especialmente en la GPU.
Vamos a realizar los cálculos tanto para operaciones de punto flotante en 32 bits (FP32) como para 64 bits (FP64) en el procesador y la GPU de la MSI GS65 Stealth Thin 8RF.
CPU: Intel Core i7-8750H
Cálculo para FP32 (32 bits):
Núcleos: 6
Frecuencia turbo: 4.1 GHz = 4.1 x 10⁹ Hz
Operaciones por ciclo (AVX2): 16 operaciones FP32 por ciclo por núcleo.
FLOPS_CPU-FP32 = 6 núcleos × 4.1 × 10^9 Hz × 16 operaciones por ciclo = 393.6 GFLOPS
Cálculo para FP64 (64 bits):
Operaciones por ciclo (AVX2 en FP64): Por cada operación de 64 bits, se realizan la mitad de operaciones que en 32 bits, es decir, 8 operaciones por ciclo.
FLOPS_CPU-FP64 = 6 núcleos × 4.1 × 10^9 Hz × 8 operaciones por ciclo = 196.8 GFLOPS
GPU: NVIDIA GTX 1070 Max-Q
Cálculo para FP32 (32 bits):
FLOPS (FP32) = 2,048 núcleos × 1.215 GHz × 2 operaciones por ciclo
= 2,048 × 1.215 × 2
= 4,976.64 GFLOPS
= 4.976 TFLOPS
Cálculo para FP64 (64 bits): La mayoría de las GPUs orientadas a gráficos, como la GTX 1070 Max-Q, tienen un rendimiento mucho menor en FP64. El ratio típico para esta tarjeta es de 1/32 del rendimiento de FP32. Por lo tanto:
FLOPS (FP64) = 2,048 núcleos × 1.215 GHz × 2/32 operaciones por ciclo
= 2,048 × 1.215 × 0.0625
= 155.52 GFLOPS
= 0.155 TFLOPS
Resumen de los resultados
Tipo de operación |
CPU (GFLOPS) |
GPU (GFLOPS) |
Total (GFLOPS) |
|---|---|---|---|
FP32 (32 bits) |
393.6 |
4,976.64 |
5370.24 |
FP64 (64 bits) |
196.8 |
155.52 |
352.32 |
De esta forma, el rendimiento máximo teórico en operaciones de punto flotante de 32 bits (FP32) es aproximadamente 5370.24 GFLOPS, mientras que para operaciones de 64 bits (FP64) sería de 352.32 GFLOPS.