Medidas de desempeño#
En esta Clase vamos a repasar, de manera práctica, los conceptos de medidas de desempeño#
Tiempos de ejecución#
Es la métrica más sencilla, solo tenemos que calcular el tiempo desde que empieza a correr el programa hasta que termina.
import time
def funcion(tiempo: int):
time.sleep(tiempo)
inicio = time.time()
funcion(10)
fin = time.time()
print(f"El tiempo de ejecución del código es de {fin- inicio}")
# Podemos notar que el tiempo de ejecución es diferente a los que podríamos suponer.
# Aunque la funcion se va a dormir por 10 segundos, el programa tarda un tiempo más en enviar las instrucciones a la ALU para hacer el proceso.
El tiempo de ejecución del código es de 10.00997519493103
Aceleración#
Esta métrica mide la rapidéz con la que se ejecuta un algoritmo paralelo respecto a como se haría en (1 procesador).
Si tenemos un algoritmo que emplea 60 segundos en completar su ejecución con un solo procesador, cuanto es la aceleración del algoritmo si con 4 procesadores la realiza en 20 segundos.
t_1 = 60
t_4 = 20
Aceleracion = 60/20
print(f" La aceleración es de {Aceleracion} veces")
#La aceleración de un algoritmo es adimensional
La aceleración es de 3.0 veces
# Si tenemos los tiempos del algoritmo, ejecutado con diferentes procesadores
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
n_cores = np.array([2,4,8,16,32,64,128])
t_paralelo = np.array([45,20,15,8,5.11,2.3,0.8])
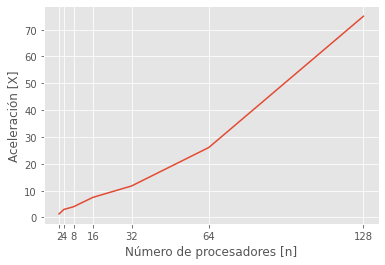
# Miremos gráficamente el comportamiento.
acel = t_1 / t_paralelo
plt.plot(n_cores, acel)
plt.xticks(n_cores);
plt.ylabel("Aceleración [X]");
plt.xlabel("Número de procesadores [n]");
plt.figure()
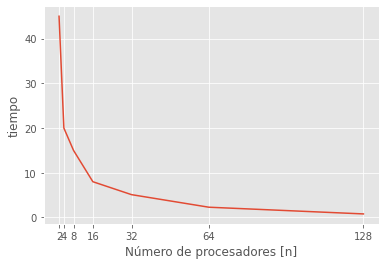
plt.plot(n_cores, t_paralelo)
plt.xticks(n_cores);
plt.ylabel("tiempo");
plt.xlabel("Número de procesadores [n]");
Eficiencia#
Supongamos que tenemos un problema que se puede resolver en 100 segundos con un algoritmo secuencial. Queremos resolver el mismo problema utilizando un algoritmo paralelo en una computadora con 4 procesadores. Ejecutamos el algoritmo paralelo y medimos que tarda 25 segundos en completar.
import numpy as np
t_secuencial = 100
t_para = [100,60,34,25,20,14,8]
proc = np.array([1,2,4,8,16,32,64])
eficiencia = t_secuencial /(proc * t_para) ## Esta se deduce de la ecn de aceleración y eficiencia.
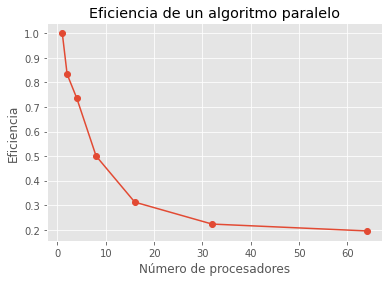
plt.plot(proc,eficiencia,'-o')
plt.xlabel('Número de procesadores')
plt.ylabel('Eficiencia')
plt.title('Eficiencia de un algoritmo paralelo')
plt.show()
Ley de Amdahl#
supongamos que tenemos un programa secuencial que tarda 1 hora en completarse, y que podemos paralelizar el 50% del código. Es decir, la mitad del programa se puede ejecutar en paralelo, mientras que la otra mitad sigue siendo secuencial. Si tenemos 8 procesadores disponibles para ejecutar el programa en paralelo, ¿cuál sería el tiempo de ejecución?
Para responder a esta pregunta, podemos utilizar la Ley de Amdahl y la siguiente fórmula:
\begin{align}{ {\huge Acel = \frac{1}{f_s + (\frac{f_p}{N})}} }\end{align}
Acá \(f_s\) es la fracción secuencial
Acá \(f_p\) es la fracción paralela
Acá \(N\) es la cantidad de procesadores
N = 8
frac_ser = 0.5
frac_par = 1 - frac_ser
acel = 1/(frac_ser +(frac_par/N))
acel
1.7777777777777777
#s=ts/tp;
#tp=ts/s
tp=60/1.7777
tp
33.751476627102434
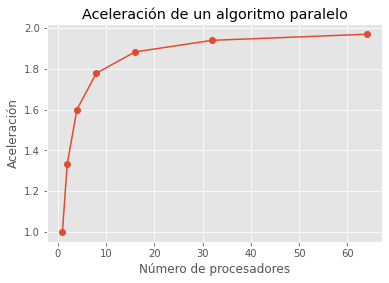
## Ahora miremos el desempeño del algoritmo variando el número de procesadores
import numpy as np
N = np.array([1,2,4,8,16,32,64])
frac_ser = 0.5
frac_par = 1 - frac_ser
acel = 1/(frac_ser +(frac_par/N))
plt.plot(N,acel,'-o')
plt.xlabel('Número de procesadores')
plt.ylabel('Aceleración')
plt.title('Aceleración de un algoritmo paralelo')
plt.show()
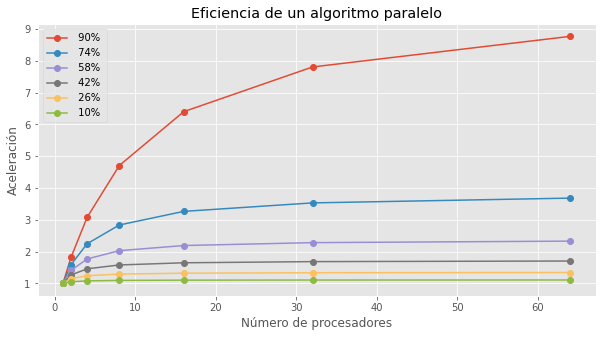
# Miremos ahora si también se modifica el porcentaje de paralelización
N = np.array([1,2,4,8,16,32,64])
frac_sers = np.linspace(0.1, 0.9, 6)
plt.figure(figsize=(10,5))
for frac_ser in frac_sers:
frac_par = 1 - frac_ser
acel = 1/(frac_ser +(frac_par/N))
plt.plot(N,acel,'-o',label=' {:.0f}% '.format(frac_par*100))
plt.xlabel('Número de procesadores')
plt.ylabel('Aceleración')
plt.title('Eficiencia de un algoritmo paralelo')
plt.legend()
plt.show()
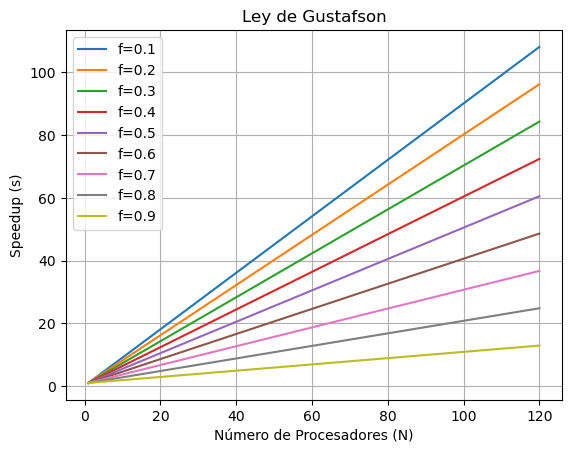
Ley de Gustafson#
Establece que cualquier problema suficientemente grande puede ser eficientemente paralelizado, ofrece un nuevo punto de vista y así una visión positiva de las ventajas del procesamiento paralelo. La ecuación \(s\) se define de la siguiente manera:
Donde:
\(f\) es el porcentaje en decimales de la parte secuencial.
\(N\) es la cantidad de procesadores.
import matplotlib.pyplot as plt
import numpy as np
# Valores de N (número de procesadores) de 1 a 120
N = np.arange(1, 121)
# Valores de f (fracción secuencial) desde 0.1 hasta 0.9
f_values = np.linspace(0.1, 0.9, 9)
# Crear un gráfico para cada valor de f
for f in f_values:
speedup = N - f * (N - 1)
plt.plot(N, speedup, label=f'f={f:.1f}')
# Configurar el gráfico
plt.xlabel('Número de Procesadores (N)')
plt.ylabel('Speedup (s)')
plt.title('Ley de Gustafson')
plt.legend()
plt.grid()
# Mostrar el gráfico
plt.show()
Ejercicio#
Establezca el porcentaje de paralelización de un algoritmo que tiene:
Aceleración = 2.3 X
Procesadores = 12
Pista: Utilice la Ley de Amdahl
### TU CÓDIGO VA AQUÍ
S=2.3
N=12
fs=(N-S)/(S*(N-1))
fp=1-fs
print("el procentaje de codigo paralelo es: ",fp*100)
### HASTA AQUÍ
el procentaje de codigo paralelo es: 61.6600790513834
Ejercicio de Aceleraciones#
#@title Ejecute la siguente celda para importar los insumos del ejercicio
import time
t_secuencial = 60 #@param
t_paralelo = 5 #@param
t_exportdata = 3*60 #@param
def leerdata():
time.sleep(1)
def asignarMemoria():
time.sleep(1)
def copiarDatos():
time.sleep(1)
def kernelSecuencial(t:int=t_secuencial):
time.sleep(t)
def kernelParalelo(t:int=t_paralelo):
time.sleep(t)
def exportarDatos(t:int=t_exportdata):
time.sleep(t)
def liberarMemoria():
time.sleep(1)
Un proceso a bajo nivel de paralelización de un proceso consta de varias etapas en el siguiente orden:
Leer data en RAM de CPU
Asignar memoria en la GPU
Copiar datos de la RAM de CPU a RAM de GPU y cache
Ejecución de la tarea (paralelo o serial)
Exportar datos de la GPU a la CPU
Liberar memoria
Simulemos un proceso secuencial y un programa paralelizado
para eso pueden usar las siguientes funciones:
* leerdata()
* asignarMemoria()
* copiarDatos()
* kernelSecuencial()
* kernelParalelo()
* exportarDatos()
* liberarMemoria()
Teniendo estas funciones, arme dos casos, un proceso secuencial y un proceso paralelizado; luego realice la medición de los “breakdowns” y tiempos de ejecución del kernel.
Calcule la aceleración del programa paralelizado respecto al secuencial.
Calcule la fracción de código paralelo y no paralelo con respecto al tiempo.
Analice el comportamiento de la aceleración de todo el programa o de solo la parte de kernel. ¿Vale la pena la paralelización?
Vaya al formulario y multiplique el “t_exportdata” por 60. Realice los pasos anteriores en otra celda, analice los cambios y concluya sobre los resultados
### parte 1,2,3 - TU CÓDIGO VA ACÁ
inicio = time.time()
leerdata()
fin=time.time()
tiempoLeer=fin-inicio
inicio = time.time()
asignarMemoria()
fin=time.time()
tiempoAsignar=fin-inicio
inicio = time.time()
copiarDatos()
fin=time.time()
tiempoCopiar=fin-inicio
inicio = time.time()
kernelSecuencial()
fin=time.time()
tiempoKernelSecuencial=fin-inicio
inicio = time.time()
exportarDatos()
fin=time.time()
tiempoExportar=fin-inicio
inicio = time.time()
liberarMemoria()
fin=time.time()
tiempoLiberar=fin-inicio
totalSecuencial=tiempoLeer+tiempoAsignar+tiempoCopiar+tiempoKernelSecuencial+tiempoExportar+tiempoLiberar
print("el breakdown de tiempo es:")
print("leer data:",tiempoLeer)
print("asignar memoria:",tiempoAsignar)
print("copiar datos:",tiempoCopiar)
print("tiempo kernel secuencial:",tiempoKernelSecuencial)
print("tiempo exportar:",tiempoExportar)
print("tiempo liberar:",tiempoLiberar)
print("tiempo Total:",totalSecuencial)
### TU CÓDIGO TERMINA ACÁ
el breakdown de tiempo es:
leer data: 1.0013580322265625
asignar memoria: 1.0008609294891357
copiar datos: 1.0013360977172852
tiempo kernel secuencial: 60.05391883850098
tiempo exportar: 180.08205366134644
tiempo liberar: 1.0003104209899902
tiempo Total: 244.13983798027039
### parte 1,2,3 - TU CÓDIGO VA ACÁ
inicio = time.time()
leerdata()
fin=time.time()
tiempoLeer=fin-inicio
inicio = time.time()
asignarMemoria()
fin=time.time()
tiempoAsignar=fin-inicio
inicio = time.time()
copiarDatos()
fin=time.time()
tiempoCopiar=fin-inicio
inicio = time.time()
kernelParalelo()
fin=time.time()
tiempoKernelParalelo=fin-inicio
inicio = time.time()
exportarDatos()
fin=time.time()
tiempoExportar=fin-inicio
inicio = time.time()
liberarMemoria()
fin=time.time()
tiempoLiberar=fin-inicio
totalParalelo=tiempoLeer+tiempoAsignar+tiempoCopiar+tiempoKernelParalelo+tiempoExportar+tiempoLiberar
print("el breakdown de tiempo es:")
print("leer data:",tiempoLeer)
print("asignar memoria:",tiempoAsignar)
print("copiar datos:",tiempoCopiar)
print("tiempo kernel paralelo:",tiempoKernelParalelo)
print("tiempo exportar:",tiempoExportar)
print("tiempo liberar:",tiempoLiberar)
print("tiempo Total:",totalParalelo)
### TU CÓDIGO TERMINA ACÁ
el breakdown de tiempo es:
leer data: 1.0013678073883057
asignar memoria: 1.001302719116211
copiar datos: 1.001378059387207
tiempo kernel paralelo: 5.005009174346924
tiempo exportar: 180.10010313987732
tiempo liberar: 1.001298189163208
tiempo Total: 189.11045908927917
print("La aceleracion de todo el codigo paralelo vs secuencial es:",totalSecuencial/totalParalelo)
print("La fracción de codigo paralelo respecto al total:",tiempoKernelParalelo/totalParalelo)
print("La fracción de codigo No paralelo respecto al total:",1-tiempoKernelParalelo/totalParalelo)
print("La aceleracion de todo el codigo paralelo vs secuencial solo en el kernel es:",tiempoKernelSecuencial/tiempoKernelParalelo)
La aceleracion de todo el codigo paralelo vs secuencial es: 1.2909906683956163
La fracción de codigo paralelo respecto al total: 0.026466062207506226
La fracción de codigo No paralelo respecto al total: 0.9735339377924938
La aceleracion de todo el codigo paralelo vs secuencial solo en el kernel es: 11.998762988548783
### parte 4 - TU CÓDIGO VA ACÁ
### TU CÓDIGO TERMINA ACÁ
Ejercicio#
Usted ha sido contratado en una empresa de tecnología, y encuentra poca documentación sobre la infraestructura del cluster. Para un proceso de renovación usted debe conocer la precisión en punto flotante que tienen dos de sus computadores ya que debe dar de baja al de menor precisión. Solo tiene la siguiente información:
Computador 1:
Vel_cpu = 3 GHz
n_cpus = 128 cores
operaciones x ciclo = 4
TFlops = 49.152
Computador 2:
Vel_cpu = 3.5 GHz
n_cpus = 12 cores
operaciones x ciclo = 2
TFlops = 5.376
Computador 3:
Vel_cpu = 2.5 GHz
n_cpus = 128 cores
operaciones x ciclo = 2
TFlops = 40.96
Computador 4:
Vel_cpu = 3.5 GHz
n_cpus = 24 cores
operaciones x ciclo = 4
TFlops = 10.752
programe una función para definir el computador con la menor precisión y menor potencia
### TU CÓDIGO VA AQUÍ
### HASTA AQUÍ
Conversión de punto flotante a binario con precisión simple y doble.#
Veamos un par de funciones usando librerias para la transformación de flotante a binario.
## Conversión a binario en precisión simple.
import struct
def float_to_binary32(num):
# Estructura IEEE 754 para float de 32 bits
s = struct.pack('>f', num)
# Convierte los 4 bytes a una secuencia binaria de 32 bits
bits = ''.join(['{0:08b}'.format(b) for b in s])
return bits
float_to_binary32(-3.6245)
'11000000011001111111011111001111'
## Conversión a binario en precisión doble.
import struct
def float_to_binary64(num):
# Estructura IEEE 754 para float de 64 bits
s = struct.pack('>d', num)
# Convierte los 8 bytes a una secuencia binaria de 64 bits
bits = ''.join(['{0:08b}'.format(b) for b in s])
return bits
float_to_binary64(-3.6245)
'1100000000001100111111101111100111011011001000101101000011100101'
Ejercicio#
Teniendo en cuenta el procedimiento visto en clase para convertir de punto flotante a binario, realice un script que implemente cada uno de los pasos a pedal, sin utilizar funciones como las vistas anteriormente.
### TU CODIGO VA AQUÍ
### HASTA AQUÍ
